filmov
tv
Finding inverses of rational functions | Equations | Algebra 2 | Khan Academy

Показать описание
Keep going! Check out the next lesson and practice what you’re learning:
The inverse of a function ƒ is a function that maps every output in ƒ's range to its corresponding input in ƒ's domain. We can find an expression for the inverse of ƒ by solving the equation 𝘹=ƒ(𝘺) for the variable 𝘺. See how it's done with a rational function.
Khan Academy is a nonprofit organization with the mission of providing a free, world-class education for anyone, anywhere. We offer quizzes, questions, instructional videos, and articles on a range of academic subjects, including math, biology, chemistry, physics, history, economics, finance, grammar, preschool learning, and more. We provide teachers with tools and data so they can help their students develop the skills, habits, and mindsets for success in school and beyond. Khan Academy has been translated into dozens of languages, and 15 million people around the globe learn on Khan Academy every month. As a 501(c)(3) nonprofit organization, we would love your help!
The inverse of a function ƒ is a function that maps every output in ƒ's range to its corresponding input in ƒ's domain. We can find an expression for the inverse of ƒ by solving the equation 𝘹=ƒ(𝘺) for the variable 𝘺. See how it's done with a rational function.
Khan Academy is a nonprofit organization with the mission of providing a free, world-class education for anyone, anywhere. We offer quizzes, questions, instructional videos, and articles on a range of academic subjects, including math, biology, chemistry, physics, history, economics, finance, grammar, preschool learning, and more. We provide teachers with tools and data so they can help their students develop the skills, habits, and mindsets for success in school and beyond. Khan Academy has been translated into dozens of languages, and 15 million people around the globe learn on Khan Academy every month. As a 501(c)(3) nonprofit organization, we would love your help!
Finding inverses of rational functions | Equations | Algebra 2 | Khan Academy
Finding the inverse of a rational function
Ex: Find the Inverse of a Rational Function
Finding The Inverse Of A Rational Function (a special case)
How To Find The Inverse of a Function
How to find the inverse of a rational function
How to determine the inverse of a rational function
Finding the inverse of a rational function
MATH 1050 Final Review Fall 2024
Learn how to find the inverse of a rational function
How to Find the Inverse of a Rational Function | Algebra 2 Exercises
Finding the Inverse of a Rational Function
Inverse Function
Example to find Inverse of Rational Functions
How to Find the Inverse of a Rational Function Example 1
How to find domain and range of a rational equation using inverse
Find inverse of a rational equation with two variables in numerator and denominator
Important Inverse of Rational Function and its Domain Range
Finding inverse functions: rational | Mathematics III | High School Math | Khan Academy
Example of Finding Inverses of Rational Functions
Finding Inverses of Rational Functions
How to write the inverse of a function when it is a fraction
Inverses of Rational Functions: Checking Answers
Finding Inverses of Rational Functions
Комментарии
 0:04:17
0:04:17
 0:03:44
0:03:44
 0:03:44
0:03:44
 0:03:11
0:03:11
 0:11:36
0:11:36
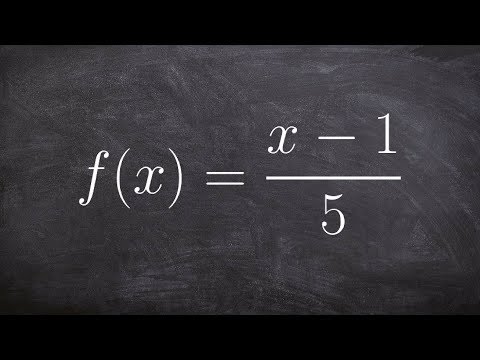 0:03:50
0:03:50
 0:05:27
0:05:27
 0:01:31
0:01:31
 1:08:28
1:08:28
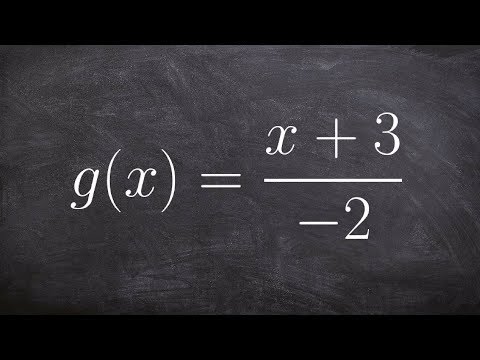 0:01:21
0:01:21
 0:04:57
0:04:57
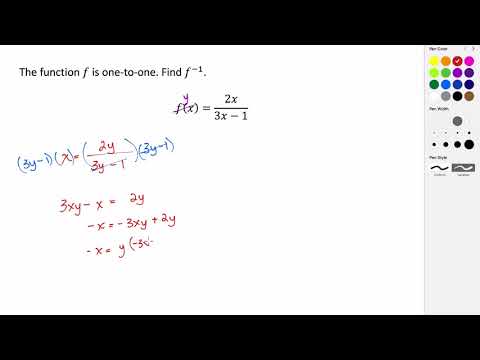 0:02:15
0:02:15
 0:01:00
0:01:00
 0:06:01
0:06:01
 0:03:51
0:03:51
 0:06:39
0:06:39
 0:04:50
0:04:50
 0:06:02
0:06:02
 0:07:01
0:07:01
 0:03:40
0:03:40
 0:21:25
0:21:25
 0:03:25
0:03:25
 0:05:19
0:05:19
 0:04:33
0:04:33