filmov
tv
Parametric Equations

Показать описание
Parametric Equations
Parametric Equations
Parametric Equations Introduction, Eliminating The Paremeter t, Graphing Plane Curves, Precalculus
Calculus 2 Lecture 10.2: Introduction to Parametric Equations
Parametric Equations in 7 minutes
Parametric Equations - How to Eliminate the Parameter
How To Find The Vector Equation of a Line and Symmetric & Parametric Equations
Parametric Equations - Some basic questions
Parametric Equations
Binomial Theorem-Finding the Constant Term
Introduction to Parametric Equations
Introduction to Parametric Equations
Intro to Plane Curves & Parametric Equations | Calculus 2 Lesson 38 - JK Math
Parametric curves | Multivariable calculus | Khan Academy
Calculus 2: Curves Defined by Parametric Equations (Video #28) | Math with Professor V
Parametric Equations : Differentiation : ExamSolutions
The Beauty of Parametric Equations! #maths
Finding Parametric Equations Passing Through Two Points
Parametric Equations
Calculus 2 Lecture 10.3: Calculus of Parametric Equations
Parametric equations
Derivatives of Parametric Functions
Introduction to Parametrics (1 of 3: Why Parameters Are Useful)
Parametric equations with sine and cosine
Converting Parametric Equation to Rectangular Form
Комментарии
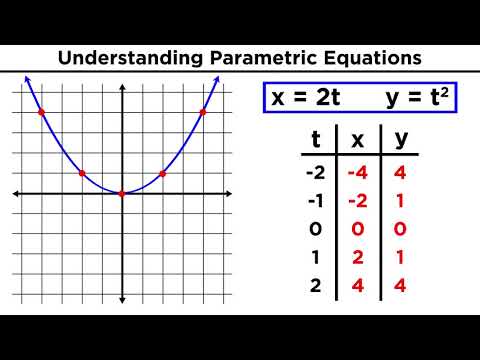 0:04:36
0:04:36
 0:33:29
0:33:29
 1:38:26
1:38:26
 0:07:39
0:07:39
 0:06:00
0:06:00
 0:11:37
0:11:37
 0:04:12
0:04:12
 0:09:53
0:09:53
 0:00:54
0:00:54
 0:30:22
0:30:22
 0:08:52
0:08:52
 0:49:05
0:49:05
 0:05:51
0:05:51
 0:31:22
0:31:22
 0:09:46
0:09:46
 0:00:19
0:00:19
 0:04:21
0:04:21
 0:07:18
0:07:18
 1:34:19
1:34:19
 0:21:54
0:21:54
 0:10:48
0:10:48
 0:09:19
0:09:19
 0:10:11
0:10:11
 0:09:23
0:09:23