Linear Programming & Combinatorial Optimization (2022) Lecture-38

In today's lecture (04/04/2022), we formalized Edmonds' Blossom Algorithm.

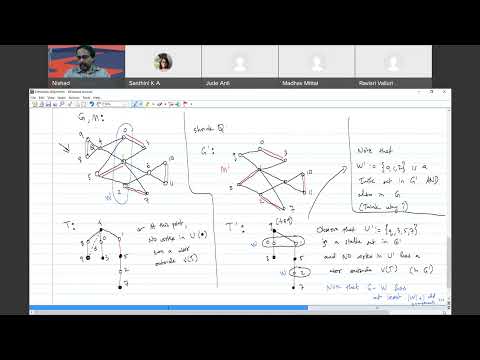
Given a graph G with some matching M, at each step of the algorithm, we've a derived graph G' (obtained from G by repeatedly shrinking blossoms --- odd cycles), a matching M' of G', and an M'-alternating tree T. We denote by U(T) the black vertices of the tree T (which includes the root), and by W(T) the white vertices of T. (Note that |U(T)| = |W(T)| + 1.)

Here is the main loop of the algorithm:

(i) IF some vertex u in U(T) has a neighbor (in G), say w, in V(G')-V(T) THEN we EITHER grow the M-alternating tree T by adding two edges (if w is M'-covered) --- uw and the M'-edge incident at w, OR (if w is M'-exposed) we find an M'-augmenting path P', we extend P' to an M-augmenting path P in G (by unshrinking the relevant blossoms recursively), we get a bigger matching M (i.e., symmetric difference of current M and P), and we reset G', M' & T appropriately (unless M is a perfect matching --- in which case, of course, we return M).

(ii) ELSE IF some two vertices u & v in U(T) are adjacent (in G') THEN we shrink the corresponding blossom (i.e, the unique odd cycle Q in T + uv) in the current G' to obtain a new G', and modify the matching M' & tree T appropriately.

(iii) ELSE the M-alternating tree T is said to be frustrated, and W(T) is a Tutte Set in G. Each node u in U(T) corresponds to a set S(u) of vertices such that G[S(u)] --- the subgraph induced by S(u) --- is an odd component of G-W(T).

In the next lecture 06/04/2022, we discuss the time complexity of Edmonds' Blossom Algorithm, and move on to discuss a Primal-Dual Algorithm for the Min Cost PM Problem in Nonbipartite Graphs.