filmov
tv
Math Olympiad Question | Which Is Larger? | You should learn this method

Показать описание
1.005^200 and 2, which one is larger? A fantastic math problem. A common method to this kind of questions.
Remind: Please give a mention If you want to use this question & the explaining steps to make videos.
Remind: Please give a mention If you want to use this question & the explaining steps to make videos.
Math Olympiad Question | You should know this trick!!
New Zealand - Math olympiad Question
A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents
A Nice Math Olympiad Exponential Equation 3^x = X^9
The unexpectedly hard windmill question (2011 IMO, Q2)
Norway Math Olympiad Question | You should be able to solve this!
Math Olympiad Question | Equation solving | You should learn this trick to pass the exam
2017 Raytheon MATHCOUNTS National Competition
Answer Key Set C IMO 2024-25/Class 9 Maths Olympiad Exam/12th Dec 2024
Luxembourg - Math Olympiad Question | You should know this trick
Germany - Math Olympiad Question
Japanese Math Olympiad Question
Math Olympiad question | Trending shorts || #shorts #youtubeshorts #short
Solve this difficult math Olympiad problem
60 years ago this question was on the International Mathematical Olympiad
Germany - Math Olympiad Question | The BEST Trick
Solving the hardest question of a British Mathematical Olympiad
Thailand | Math Olympiad Question | Nice Algebra Equation
The Legend of Question Six - Numberphile
Russian l can you solve?? l Hardest Olympiad Math Problem
IMO Maths olympiad questions | olympiad mathematics shorts | IMO MATHS OLYMPIAD
Math Olympiad Question
Math Olympiad Practice
A beautiful international math olympiad problem
Комментарии
 0:00:33
0:00:33
 0:01:12
0:01:12
 0:00:52
0:00:52
 0:02:34
0:02:34
 0:16:03
0:16:03
 0:03:21
0:03:21
 0:01:54
0:01:54
 0:56:01
0:56:01
 0:05:21
0:05:21
 0:02:51
0:02:51
 0:11:00
0:11:00
 0:10:17
0:10:17
 0:00:15
0:00:15
 0:00:10
0:00:10
 0:09:10
0:09:10
 0:10:37
0:10:37
 0:11:26
0:11:26
 0:01:26
0:01:26
 0:08:45
0:08:45
 0:18:47
0:18:47
 0:00:21
0:00:21
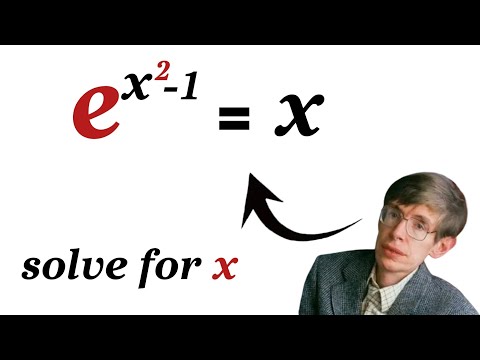 0:08:35
0:08:35
 0:01:00
0:01:00
 0:01:00
0:01:00