Trigonometry Review (1 of 5)

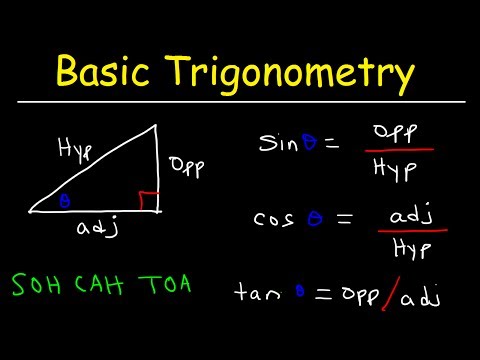
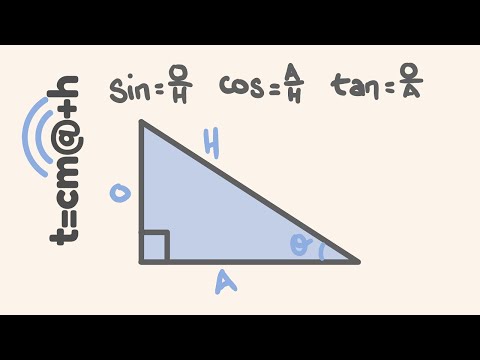
Part 1 (1-13): Convert between degrees and radians, graph angles in standard position, and find coterminal angles in both radians and degrees. Find the exact value (the ratio between the sides) of different special angles (30°-60°-90° and 45°-45°-90°) by evaluating the trigonometric function (sin, cos, tan, csc, sec, cot).

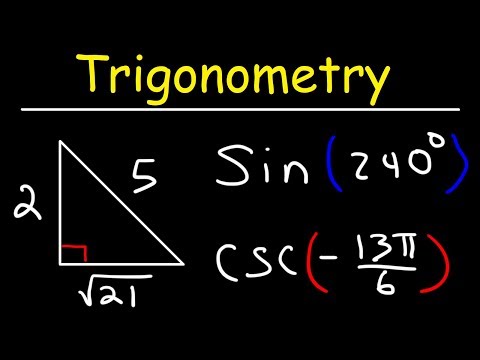
Part 2 (14-20): More evaluating questions continued from part 1. Find the trigonometric ratio given: (1) a point (x, y) on the terminal side of an angle in standard position, (2) a triangle, (3) another trig ratio. All answers are left as exact (simplified radical form).

Part 3 (20b-23): Using trig functions and inverse trig functions to find missing angles or sides in right triangles. Now we're using the calculator and approximating our answers.

Part 4 (24a-c): We leave the comfortable world of right triangles behind and enter a world with no 90° angles and no hypotenuses. So, we must use law of sines and law of cosines to find missing sides and angles and solve triangles. Beware of the SSA situation because it doesn't mean there is only 1 triangle possible; there might be two or it might not even be a triangle.

Part 5 (24d-25): We continue solving triangles with the law of sines and law of cosines. We also find the area of non-right triangles using two different area formulas.

[davidtutorsmath]

@myjuddyy You're very welcome. Thanks for taking the time to say thank you. I wish you well as you continue working with trig. I'm glad I could help you along the way. Keep asking your trig professor questions.

[sacae]

Thank you so much! You're a great teacher and your students are extremely lucky. God bless you!

[davidtutorsmath]

You're very welcome. Thanks for appreciating.

[tstbs]

Great job explaining! This definitely helps!

[-ysj]

thanks for explaining this! it really helped me!!

[davidtutorsmath]

@ProvokeLaughter Thanks for the compliment. And I will most certainly continue teaching.

[ProvokeLaughter]

You are absolutely brilliant! Keep it up!

[davidtutorsmath]

@sacae95 Thanks for the complement and taking the time to say thanks. Good luck as you study Trig.

[MrKriminal]

@davidtutorsmath oh sorry i did not notice but ur good sir it help me alot

[ladymiksits]

Number 11 should be a positive answer: negative divided by a negative = a positive

[FMMProductions]

very helpful! the only thing that confused me was how you got radical 3/2 for the long side and 1/2 for the short side. is it always like that? for every triangle? if it is that made my life much easier!
and I still didn't get how you found the first 2 co-terminal angles for the radian questions at the top. I kind of get them but I think I'll find the angles in degrees then put them into radiens, if it's okay to do that :P I figured out the degree ones though. wish me luck on my regents!

[davidtutorsmath]

@ladymiksits Yes. Thanks for reminding me. We caught it in my class the next day, and didn't correct it on here. Thanks!

[davidtutorsmath]

@MrKriminal27 You are correct, it should be positive. I'm pretty sure I had made that correction with a comment in the video. Did you see that?

[Faramar]

This just might get me through my test tomorrow :X crossing my fingers lol

[davidtutorsmath]

@MAYELOMOVIL22 Thanks. I love thinking through exact values with a visual process. It sure beat memorizing the entire unit circle.

[davidtutorsmath]

@GlenGleGlen Great! I hope you do well.

[MrKriminal]

in no 11 it should be positive square root of three.... am i right?
10:44

[davidtutorsmath]

@hellomikkii Wish I could, but I've got a job teaching students like yourself. It seems like you're on the right track with studying for it, though.

[davidtutorsmath]

@tstbs100 Great! Keep up the hard work of studying.