filmov
tv
Inverse of a Permutation | Abstract Algebra | DR Colleger

Показать описание
Inverse of a Permutation | Abstract Algebra | @drcolleger
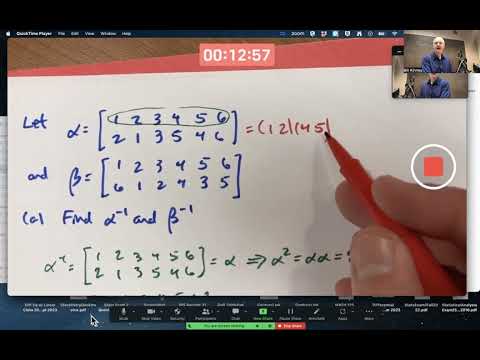
Inverse of a permutation:
Let f be a permutation on S. Since f is a bijective mapping, it admits of a unique inverse f^(-1):S→S and f^(-1) is also bijective. So f^(-1) is a permutation on S and ff^(-1)=f^(-1) f=i. If by f,a_i→a_j, then by f^(-1),a_j→a_i.
My another channel for Competitive Mathematics:
My Some Video Playlist:
Geometry :
Differential Calculus:
Set Theory:
Abstract Algebra
Linear Algebra:
Class 11 Math
Real Analysis
permutation by dr colleger,inverse of a permutation,inverse,mathematics,math,inverse function,permutation,permutations and combinations,bijective mappingpping,inverse mapping,order of permutation,even permutation,odd permutation,cycle,cycle of permutation,transposition,dr colleger,bsc math,cbcs math,cbcs mathematics semester 2,math hons and general,engineering mathematics,product of permutation,bsc math in bengali
#drcolleger
#permutation
#inverseofpermutation
#cbcsmath
#abstractalgebra
#bijectivefunction
Inverse of a permutation:
Let f be a permutation on S. Since f is a bijective mapping, it admits of a unique inverse f^(-1):S→S and f^(-1) is also bijective. So f^(-1) is a permutation on S and ff^(-1)=f^(-1) f=i. If by f,a_i→a_j, then by f^(-1),a_j→a_i.
My another channel for Competitive Mathematics:
My Some Video Playlist:
Geometry :
Differential Calculus:
Set Theory:
Abstract Algebra
Linear Algebra:
Class 11 Math
Real Analysis
permutation by dr colleger,inverse of a permutation,inverse,mathematics,math,inverse function,permutation,permutations and combinations,bijective mappingpping,inverse mapping,order of permutation,even permutation,odd permutation,cycle,cycle of permutation,transposition,dr colleger,bsc math,cbcs math,cbcs mathematics semester 2,math hons and general,engineering mathematics,product of permutation,bsc math in bengali
#drcolleger
#permutation
#inverseofpermutation
#cbcsmath
#abstractalgebra
#bijectivefunction
 0:03:32
0:03:32
 0:07:21
0:07:21
 0:03:18
0:03:18
 0:04:01
0:04:01
 0:00:49
0:00:49
 0:02:00
0:02:00
 0:03:21
0:03:21
 0:12:50
0:12:50
 0:13:23
0:13:23
 0:02:10
0:02:10
 0:00:28
0:00:28
 0:06:47
0:06:47
 0:05:22
0:05:22
 0:09:30
0:09:30
 0:04:00
0:04:00
 0:05:50
0:05:50
 0:11:01
0:11:01
 0:18:24
0:18:24
 0:01:01
0:01:01
 0:07:04
0:07:04
 0:00:55
0:00:55
 0:00:58
0:00:58
 0:08:11
0:08:11
 0:17:32
0:17:32