filmov
tv
Abstract Algebra | A PID that is not a Euclidean Domain
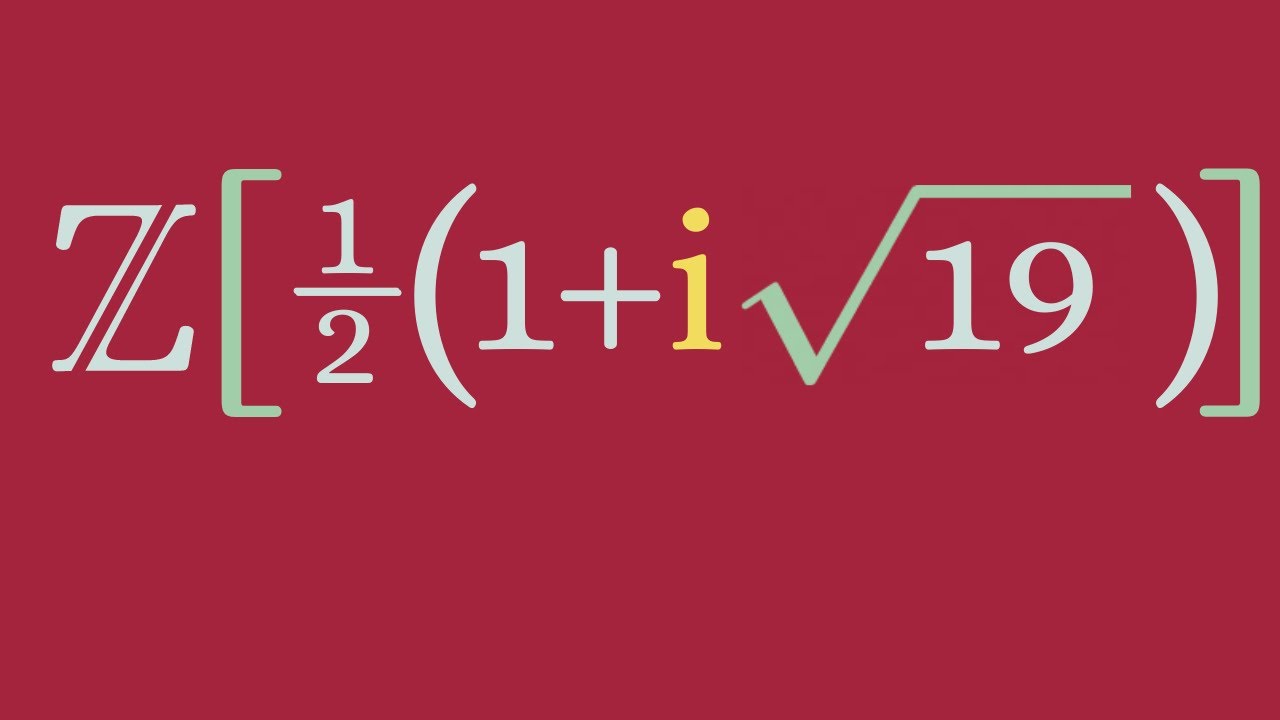
Показать описание
We present an example of a principal ideal domain that is not a Euclidean domain. We follow the outline described in Dummit and Foote. In particular, we show that an integral domain D is a PID if and only if it has a Dedekind-Hasse Norm and that every Euclidean domain has a universal side divisor. Then we show that our example has a Dedekind-Hasse norm but no universal side divisor.
Abstract Algebra | Introduction to Principal Ideal Domains (PIDs)
Abstract Algebra | k[x] is a PID
Abstract Algebra | Every PID is a UFD.
PID's are UFD's
Abstract Algebra | A PID that is not a Euclidean Domain
Principal Ideal Domain - PID - Definition - Ring Theory - Lesson 57
Abstract Algebra: PID implies UFD, extension fields begins, 11-7-18
Abstract Algebra | Introduction to Unique Factorization Domains
Abstract Algebra II: Classification of Finitely Generated Modules over PID, 4-11-22
Abstract Algebra: polynomials as sequences, PID introduced, 10-29-18
Every PID is Noetherian
Abstract Algebra 29A: Visualize Factor Rings of Gaussian Integers Z[i], Construct Complex Field C
Abstract Algebra | Ideals of quotients of PIDs
Abstract Algebra II: existence theorems of module over PID, 4-3-17 (no sound)
Abstract Algebra: irred implies prime in PID, how to find inverse in poly factor ring, 11-2-18 p2
Abstract Algebra: irred implies prime in PID, how to find inverse in poly factor ring, 11-2-18 p1
Abstract Algebra 15.3: Principal Ideal Domains
Abstract Algebra: Prime Ideals maximal in P.I.D. | THESUBNASH - Jeden Tag ein neues Mathevideo
Principal Ideal Domain - PID - Examples - Ring Theory - Lesson 58
Abstract Algebra | Introduction to Euclidean Domains
Abstract Algebra, 30B: Integral Domains: Irreducibles, Primes, PIDs, UFDs, Fermat's Last Thm, E...
Abstract Algebra: ED implies PID implies UFD, some number theory, 11-29-17
Abstract Algebra: PIDs, irreducible iff maximal theorem for poly over ID, 10-31-18
Abstract Algebra II: structure theorems for finitely generated modules over PID, 4-23-18
Комментарии
 0:18:27
0:18:27
 0:10:03
0:10:03
 0:25:31
0:25:31
 0:16:59
0:16:59
 0:36:49
0:36:49
 0:07:33
0:07:33
 0:51:40
0:51:40
 0:11:08
0:11:08
 0:31:34
0:31:34
 0:50:11
0:50:11
 0:04:46
0:04:46
 0:36:29
0:36:29
 0:23:33
0:23:33
 0:51:07
0:51:07
 0:07:11
0:07:11
 0:59:51
0:59:51
 0:05:15
0:05:15
 0:04:53
0:04:53
 0:15:32
0:15:32
 0:17:11
0:17:11
 0:27:01
0:27:01
 0:51:13
0:51:13
 0:52:31
0:52:31
 0:46:26
0:46:26