filmov
tv
Abstract Algebra, 30B: Integral Domains: Irreducibles, Primes, PIDs, UFDs, Fermat's Last Thm, EDs
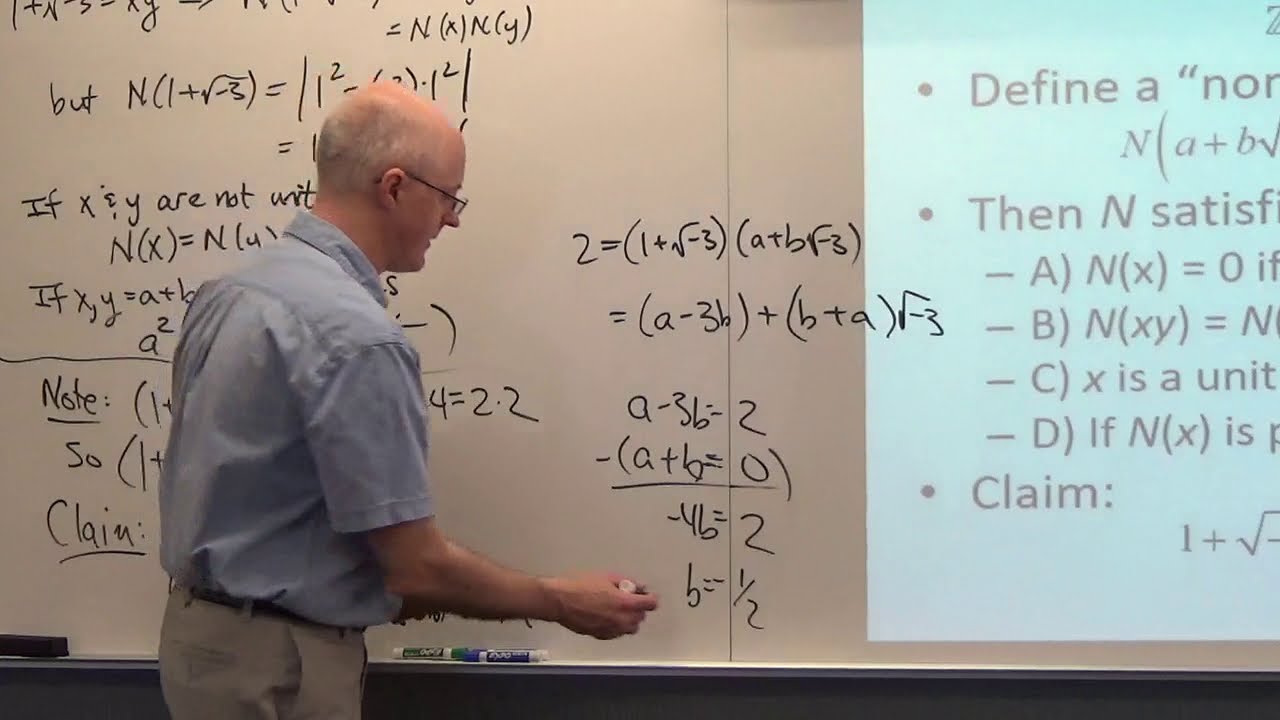
Показать описание
(0:00) Proof that 1+sqrt(-3) is irreducible but not prime in Z[sqrt(-3)].
(4:49) Theorems relating irreducible elements and prime elements in integral domains and principal ideal domains.
(6:51) Unique factorization domains.
(8:55) Every PID is a UFD (so F[x] is a UFD, where F is a field).
(10:19) Z[x] is a UFD even though it is not a PID.
(12:30) Z[sqrt(-5)] is not even a UFD (for example, 21 does not factor uniquely as a product of irreducibles).
(14:01) History of Fermat's Last Theorem leading up to Andrew Wiles' proof (also note contributions from Jean Luc Picard and Homer Simpson...lol ).
(21:14) Brief overview of Euclidean domains (including the facts that every ED is a PID and therefore every ED is also a UFD; if D is a UFD, then D[x] is a UFD (like for D = Z); the Gaussian integers Z[i] form an ED).
(23:00) Mathematica code to visualize Z[sqrt(d)], when d is negative, and the level curves (contour map) of the norm N (with formula N(a + b*sqrt(d)) =a^2 + d*b^2).
AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.
Abstract Algebra, 30B: Integral Domains: Irreducibles, Primes, PIDs, UFDs, Fermat's Last Thm, E...
Abstract Algebra, Lec 30A: Divisibility in Integral Domains: Associates, Irreducibles, Primes, Norms
Norms of an Integral Domains
Irreducibility & Reducibility of Polynomials Over Integral Domains & Fields (Definition, Exs...
Abstract Alg, Lec 31A: Review Special Integral Domains: UFDs, PIDs, EDs (also Irreducibles, Primes)
Group Theory 84, Associates, Irreducibles and Primes
UFDsIV
Unique Factorization domains is a Integrally closed domains
UFDsV
Abstract Algebra: help session, 11-15-16
Abstract Algebra, Lec 31B: Z[sqrt(-5)] is not a UFD, Exam 3 Review: (Mostly) Ring Theory
Problems in Mathematics: Abstract Algebra-9
Math 706 Sections 2.12-2.13
Examples of Euclidean Domains II (Algebra 2: Lecture 3 Video 4)
Commutative algebra 9 (Euclidean domains)
Examples of Euclidean Domains I (Algebra 2: Lecture 3 Video 3)
Primes and Irreducibles Part 2
Abstract Algebra: ED implies PID implies UFD, some number theory, 11-29-17
Group Theory 85, Irreducible but not a prime
An Irreducible Element that is Not a Prime
Abstract algebra section 1.7. Unique factorization in domain of integers
Z and F[x] are PIDs (Algebra 2: Lecture 3 Video 1)
Euclidean Domains and Norm
Lecture 7 part 1
Комментарии
 0:27:01
0:27:01
 0:36:07
0:36:07
 0:12:41
0:12:41
 0:16:09
0:16:09
 0:36:34
0:36:34
 0:06:20
0:06:20
 0:10:11
0:10:11
 0:05:31
0:05:31
 0:13:43
0:13:43
 0:56:03
0:56:03
 0:30:19
0:30:19
 0:02:40
0:02:40
 0:15:55
0:15:55
 0:11:09
0:11:09
 0:25:55
0:25:55
 0:22:40
0:22:40
 0:16:56
0:16:56
 0:51:13
0:51:13
 0:12:24
0:12:24
 0:08:04
0:08:04
 0:06:17
0:06:17
![Z and F[x]](https://i.ytimg.com/vi/kZzxplQH2Hk/hqdefault.jpg) 0:13:59
0:13:59
 0:22:03
0:22:03
 0:12:08
0:12:08