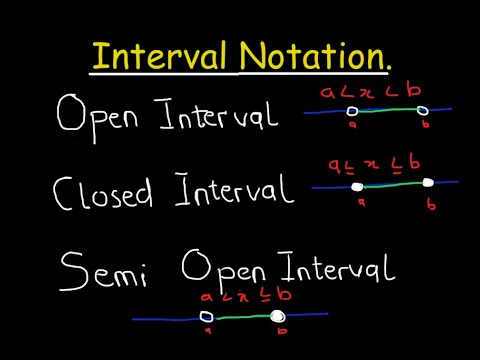
interval notation . Closed ,open and semi open intervals.

Показать описание

Interval notation is a way to describe continuous sets of real numbers by the numbers that bound them. Intervals, when written, look somewhat like ordered pairs. However, they are not meant to denote a specific point. Rather, they are meant to be a shorthand way to write an inequality or system of inequalities.

In mathematics, a (real) interval is the set of all real numbers lying between two fixed endpoints with no "gaps". Each endpoint is either a real number or positive or negative infinity, indicating the interval extends without a bound. An interval can contain neither endpoint, either endpoint, or both endpoints.

An interval is a subset of the real numbers that contains all real numbers lying between any two numbers of the subset.
The endpoints of an interval are its supremum, and its infimum, if they exist as real numbers.[1] If the infimum does not exist, one says often that the corresponding endpoint is
−
∞
.
{\displaystyle -\infty .} Similarly, if the supremum does not exist, one says that the corresponding endpoint is
+
∞
.
{\displaystyle +\infty .}
Intervals are completely determined by their endpoints and whether each endpoint belong to the interval. This is a consequence of the least-upper-bound property of the real numbers. This characterization is used to specify intervals by mean of interval notation, which is described below.
An open interval does not include any endpoint, and is indicated with parentheses.[2] For example,

is the interval of all real numbers greater than 0 and less than 1. (This interval can also be denoted by ]0, 1[, see below). The open interval (0, +∞) consists of real numbers greater than 0, i.e., positive real numbers. The open intervals are thus one of the forms

A closed interval is an interval that includes all its endpoints and is denoted with square brackets.[2] For example, [0, 1] means greater than or equal to 0 and less than or equal to 1. Closed intervals have one of the following forms in which a and b are real numbers such that

An interval is said to be left-bounded or right-bounded, if there is some real number that is, respectively, smaller than or larger than all its elements. An interval is said to be bounded, if it is both left- and right-bounded; and is said to be unbounded otherwise. Intervals that are bounded at only one end are said to be half-bounded. The empty set is bounded, and the set of all reals is the only interval that is unbounded at both ends. Bounded intervals are also commonly known as finite intervals.

Bounded intervals are bounded sets, in the sense that their diameter (which is equal to the absolute difference between the endpoints) is finite. The diameter may be called the length, width, measure, range, or size of the interval. The size of unbounded intervals is usually defined as +∞, and the size of the empty interval may be defined as 0 (or left undefined).

However, there is conflicting terminology for the terms segment and interval, which have been employed in the literature in two essentially opposite ways, resulting in ambiguity when these terms are used. The Encyclopedia of Mathematics[7] defines interval (without a qualifier) to exclude both endpoints (i.e., open interval) and segment to include both endpoints (i.e., closed interval), while Rudin's Principles of Mathematical Analysis[8] calls sets of the form [a, b] intervals and sets of the form (a, b) segments throughout. These terms tend to appear in older works; modern texts increasingly favor the term interval (qualified by open, closed, or half-open), regardless of whether endpoints are included.