filmov
tv
Uniqueness and stability for an inverse Steklov problem

Показать описание
(22 mars 2021 / March 22, 2021) Young researchers in spectral geometry II (Mini-conférence)
Germain Gendron (Université de Nantes, France)
Uniqueness and stability for an inverse Steklov problem
Abstract:
In this talk, we present results for an inverse Steklov problem for a particular class of 2-dimensional manifolds having the topology of a hollow sphere and equipped with a warped product metric. We prove that the knowledge of the Steklov spectrum determines uniquely the associated warping function up to a natural invariance. Then, we study the continuous dependence of the warping function defining the warped product with respect to the Steklov spectrum.
Germain Gendron (Université de Nantes, France)
Uniqueness and stability for an inverse Steklov problem
Abstract:
In this talk, we present results for an inverse Steklov problem for a particular class of 2-dimensional manifolds having the topology of a hollow sphere and equipped with a warped product metric. We prove that the knowledge of the Steklov spectrum determines uniquely the associated warping function up to a natural invariance. Then, we study the continuous dependence of the warping function defining the warped product with respect to the Steklov spectrum.
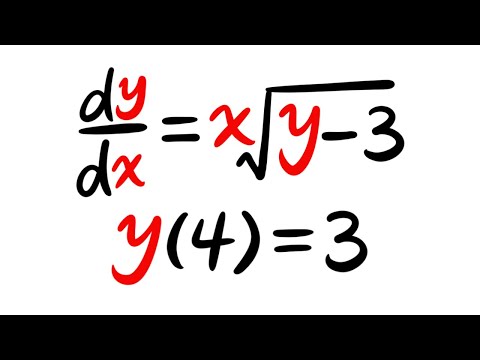 0:11:22
0:11:22
 0:47:02
0:47:02
 0:12:22
0:12:22
 0:07:23
0:07:23
 0:09:28
0:09:28
 0:26:57
0:26:57
 0:44:32
0:44:32
 0:14:02
0:14:02
 0:07:23
0:07:23
 0:21:43
0:21:43
 0:11:29
0:11:29
 0:26:02
0:26:02
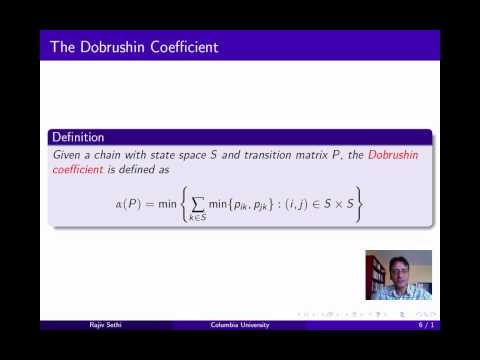 0:11:11
0:11:11
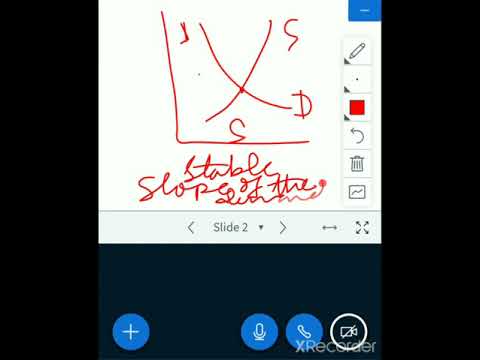 0:22:51
0:22:51
 0:13:47
0:13:47
 1:01:56
1:01:56
 1:19:19
1:19:19
 0:06:21
0:06:21
 0:00:15
0:00:15
 0:08:16
0:08:16
 0:06:58
0:06:58
 0:53:05
0:53:05
 0:12:35
0:12:35
 0:32:28
0:32:28