filmov
tv
Can you solve this calculus problem?
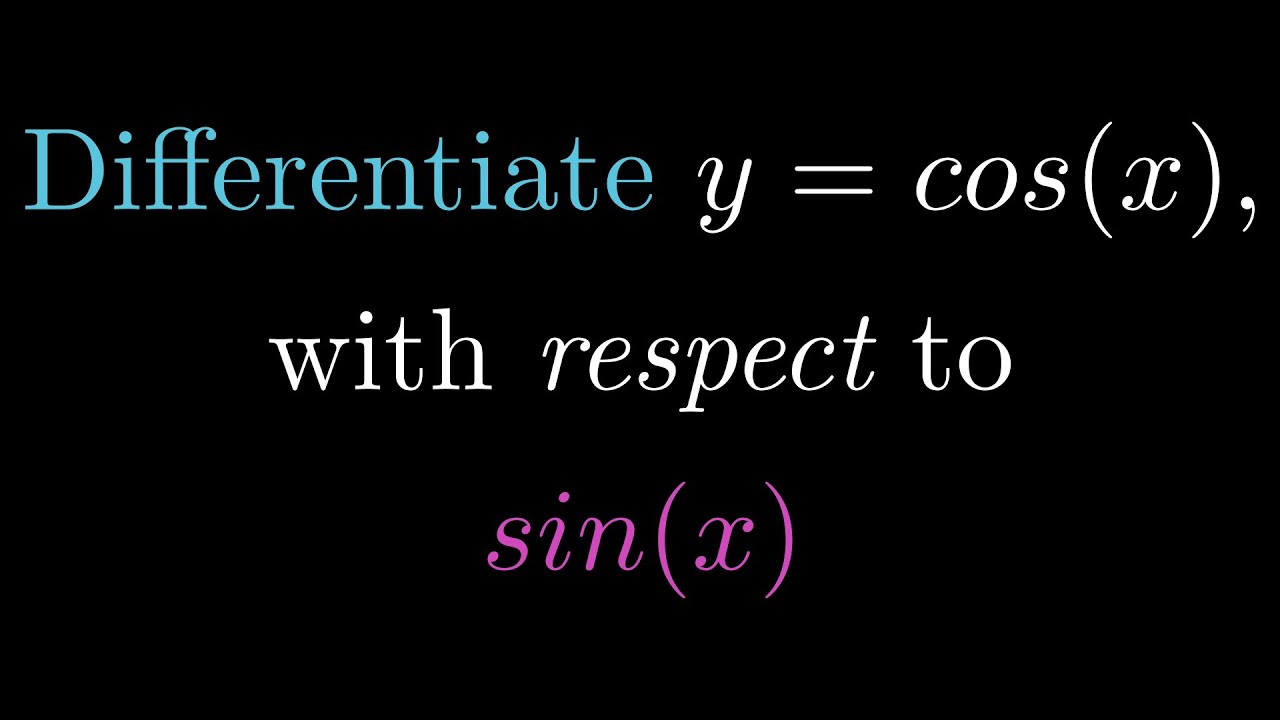
Показать описание
In this video we solve another tricky derivative problem!
Learn to Solve an Integral (What Makes You Beautiful Parody) AP Calculus BC
The Most Useful Calculus 1 Tip!
Understanding Calculus in One Minute... 🤯
How did I learn Calculus?🤔 w/ Neil deGrasse Tyson
Math Integration Timelapse | Real-life Application of Calculus #math #maths #justicethetutor
Understand Calculus in 1 minute
I Wish I Saw This Before Calculus
Infinite Limit Shortcut!! (Calculus)
Nice square root explanation! #maths #mathproblem #algebra #mathstricks #mathematics #squareroot
Integration (Calculus)
Can you solve this equation?
Understand Calculus in 35 Minutes
BASIC Math Calculus – Understand Simple Calculus with just Basic Math in 5 minutes!
integration by parts is easy
How REAL Men Integrate Functions
You're a physicist, so you're good at math, right? #Shorts
Calculus SPEEDRUN (U-Sub)!!
MASTER Derivatives In Less Than A Minute!!
Your First Basic CALCULUS Problem Let’s Do It Together….
Solving limits by factoring | Calculus Tutorial and Help
Finding the Derivative of a Polynomial Function | Intro to Calculus #shorts #math #maths
Calculus - Introduction to Calculus
Calculus 1 - Introduction to Limits
Japanese | Super Square Root Algebra Problem | Math Olympaid || Can you solve this?
Комментарии
 0:03:39
0:03:39
 0:00:10
0:00:10
 0:00:52
0:00:52
 0:00:59
0:00:59
 0:00:09
0:00:09
 0:00:57
0:00:57
 0:00:43
0:00:43
 0:00:51
0:00:51
 0:00:50
0:00:50
 0:07:04
0:07:04
 0:00:28
0:00:28
 0:36:22
0:36:22
 0:08:20
0:08:20
 0:00:33
0:00:33
 0:00:35
0:00:35
 0:00:09
0:00:09
 0:01:00
0:01:00
 0:00:58
0:00:58
 0:20:46
0:20:46
 0:00:42
0:00:42
 0:01:01
0:01:01
 0:04:11
0:04:11
 0:20:20
0:20:20
 0:09:04
0:09:04