filmov
tv
6 minutes of Fascinating Math
Показать описание
Math can sometimes be fascinating.
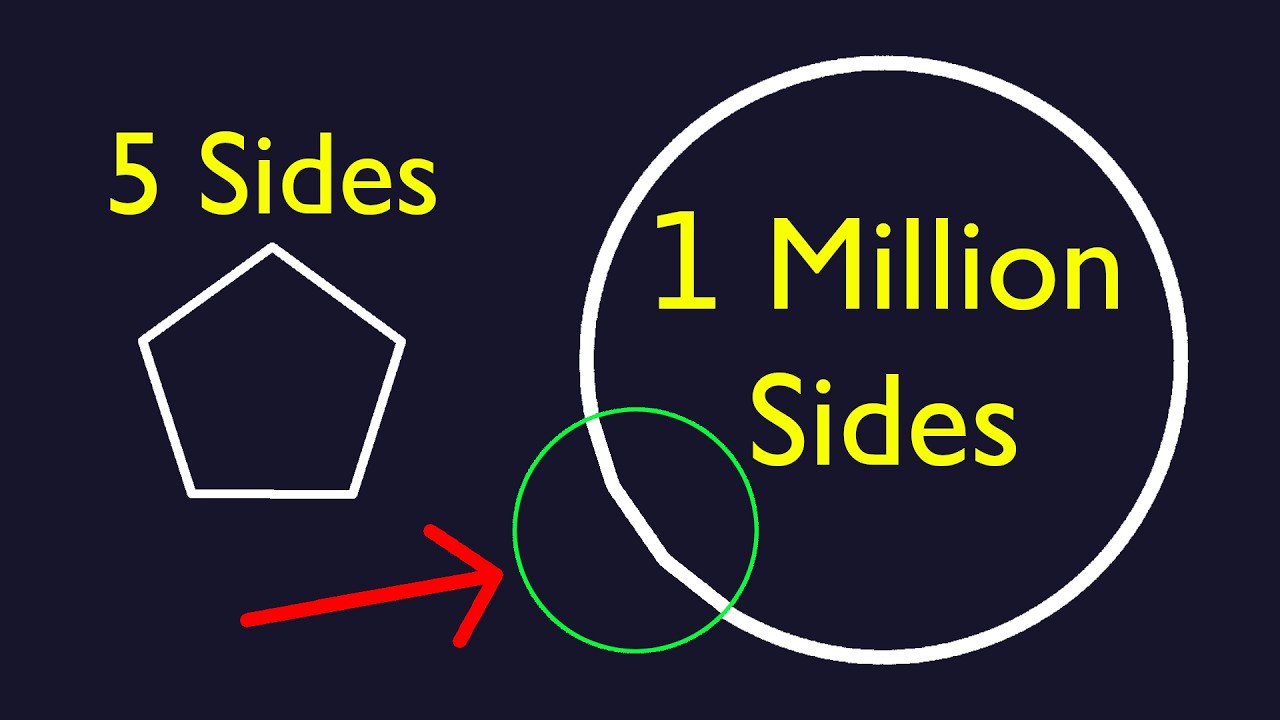
6 minutes of Fascinating Math
4 𝙢𝙞𝙣𝙪𝙩𝙚𝙨 𝙤𝙛 𝙄𝙉𝙏𝙀𝙍𝙀𝙎𝙏𝙄𝙉𝙂 𝙈𝘼𝙏𝙃...
Amazing Math Hacks
The most dangerous problem in math
simple math
HOW CHINESE STUDENTS SO FAST IN SOLVING MATH OVER AMERICAN STUDENTS
The Oldest Unsolved Problem in Math
Fast Multiplication Trick | Interesting math tricks #maths #shorts
Arithmetic Progressions | Exercise-5.2 | Problem - 12 | Chapter-5 |CBSE |Class-10|Math #cbseclass10
The Hardest Math Test
If you are a genius solve this! Math Game Challenge!!!
Every Weird Math Paradox
The Simplest Math Problem No One Can Solve - Collatz Conjecture
Proving God exists using Math
Mental Math Tricks
Every Type of Math Explained in 9 Minutes.
9 Math Riddles That'll Stump Even Your Smartest Friends
6 x 6 = 36 #math #multiplication
The benefits of doing nothing ⏲️ 6 Minute English
Memorization Trick for Graphing Functions Part 1 | Algebra Math Hack #shorts #math #school
Math Integration Timelapse | Real-life Application of Calculus #math #maths #justicethetutor
9 TIMES TABLE #shorts #math #maths #mathematics
The World’s Hardest Math Class
Genius math craft ✏️ #shorts
Комментарии
 0:06:35
0:06:35
 0:04:35
0:04:35
 0:00:16
0:00:16
 0:01:00
0:01:00
 0:00:12
0:00:12
 0:00:23
0:00:23
 0:31:33
0:31:33
 0:00:28
0:00:28
 0:04:38
0:04:38
 0:00:28
0:00:28
 0:00:28
0:00:28
 0:11:15
0:11:15
 0:22:09
0:22:09
 0:05:23
0:05:23
 0:00:27
0:00:27
 0:08:50
0:08:50
 0:06:40
0:06:40
 0:00:21
0:00:21
 0:06:20
0:06:20
 0:00:15
0:00:15
 0:00:09
0:00:09
 0:00:23
0:00:23
 0:00:34
0:00:34
 0:00:53
0:00:53