filmov
tv
Sum and Product of Roots

Показать описание
How To Find The Sum and Product of the Roots of a Quadratic Equation - Algebra
Sum & Product of Roots (Polynomials) [IB Math AA HL]
Sum and Product of Roots
Writing Quadratic Equations Given The Sum and Product of the Roots - Algebra
Sum and Product of the Roots of Quadratic Equation - Finding the Quadratic Equation
Sum and Product of Roots - Example 1
Sum & Product of Roots (3 of 5: Basic example questions)
Finding the Sum and Product of the Roots of Quadratic Equation I Explain in Detailed |
GRADE 9 MATHEMATICS👉 Quarter 1 Reviewer for Periodical Test (Multiple Choice)
Sum and Product of Roots | Symmetrical Functions of root
How to find the sum and product of roots of a quadratic equation #algebra
Sum and Product of Roots of a Quadratic Equation
A Maths Chap 3.1 Sum and Product of Roots - Example 1
Finding polynomial whose sum and product of roots is given | Polynomial | Math | Khan Academy
Sum & Product of Roots (5 of 5: Forming a quadratic with given roots)
Finding Sum of Roots (SOR) and Product of Roots (POR) of the Equations
How to Find Sum and Product of Roots of Quadratic Equations Urdu || Sir Naimat
Proof of Sum and Product of roots of Quadratic Equations
📌PAANO mag SOLVE ng SUM and PRODUCT of ROOTS ng QUADRATIC EQUATIONS I HOW TO I Tagalog Math I SIR OW...
Deriving the Formulas in Finding the Sum and the Product of the Roots of a Quadratic Equation
Finding the Sum and Product of the Roots of Quadratic Equations - Grade 9 Mathematics
How to derive formulas of the roots of Quadratic Equations
Sum and Product of Roots of Quadratic Equations | Grade 9 MELC
Sum of polynomial roots (proof) | Math for fun and glory | Khan Academy
Комментарии
 0:10:43
0:10:43
 0:04:06
0:04:06
 0:09:37
0:09:37
 0:11:15
0:11:15
 0:10:22
0:10:22
 0:09:27
0:09:27
 0:10:30
0:10:30
 0:14:56
0:14:56
 0:09:11
0:09:11
 0:09:55
0:09:55
 0:00:48
0:00:48
 0:26:57
0:26:57
 0:06:02
0:06:02
 0:02:42
0:02:42
 0:08:19
0:08:19
 0:09:17
0:09:17
 0:02:47
0:02:47
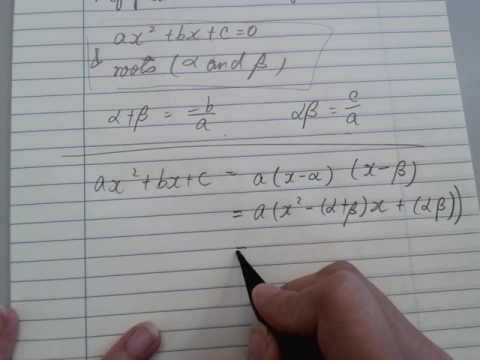 0:02:05
0:02:05
 0:11:07
0:11:07
 0:07:19
0:07:19
 0:09:47
0:09:47
 0:25:54
0:25:54
 0:04:41
0:04:41
 0:14:47
0:14:47