filmov
tv
1959 IMO (Romania) | Problem 2
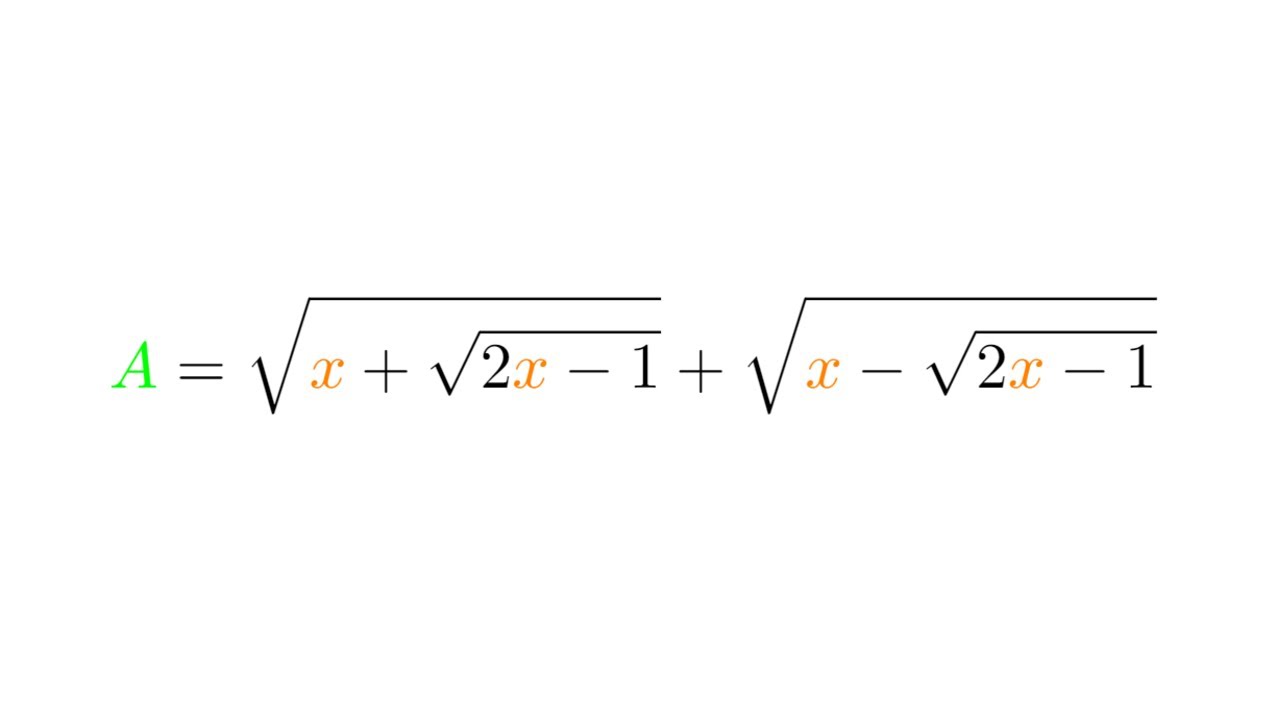
Показать описание
We take a look at an IMO Problem from 1959 proposed in Romania describing an algebraic equation with square roots and analyzing the cases with the given conditions the question has provided for us.
Thanks for watching. Like, comment, and subscribe for more content in the future!
Instagram:
Music by order:
GYVUS - Lemon Tea
Thanks for watching. Like, comment, and subscribe for more content in the future!
Instagram:
Music by order:
GYVUS - Lemon Tea
0:10:53
1959 IMO (Romania) | Problem 2
0:08:41
IMO 1959 - Problem 2
0:13:19
[Very first IMO in history] 1959 IMO Problem #3: Quadratic Equation in cos(x)
0:10:08
The First International Math Olympiad Problem [IMO 1959 Problem 1]
0:03:34
IMO 1959 Problem 1.
0:04:09
IMO 1959 Problem 1
0:07:55
IMO Problems from old days (1959-Problem 3)
0:11:27
[Very first IMO in history] 1959 IMO Problem #5: Circles, Squares, and Locus
0:19:46
IMO 1959 Problem 1
0:07:50
First International Maths Olympiad Question | IMO 1959 | Proof by Absurdity or Contradiction
0:04:43
(EASIEST Problem on the HARDEST Test) 1959 IMO Problem 1 | First International Math Olympiad Problem
0:24:34
International Mathematical Olympiad (IMO) 1959 - Solutions
0:08:06
1964 IMO Problem #4
0:15:50
Classical IMO problem from 1959
0:07:04
IMO - 1959 - Problema 1 - TEORIA DOS NÚMEROS
0:08:09
The very first International Math Olympiad Problem | IMO 1959 Q2 Solution l #imo1959 #maths
0:11:09
1st IMO- Romania- 1959 - Irreducibility of fractions
0:03:53
El primer problema de la primer IMO - IMO 1959 problema 1
0:10:37
Two proofs to an easy number theory problem from IMO 1959. USE HEADPHONE FOR BETTER QUALITY
0:16:27
IMO 1959 - Problème n°3
0:17:46
IMO First Problem Ever! (one-liner solution?) | International Math Olympiad 1959 Problem 1
0:04:06
FIRST International Math Olympiad Problem, Romania 1959, Show f(n) equals fraction is irreducible
0:06:41
INTERNATIONAL MATHEMATICAL OLYMPIAD 1959 | ALGEBRA CHALLENGE
0:08:06
IMO 1959 - Problème n°2
Комментарии