filmov
tv
Parametric Curves: Example 7: The Cycloid: Proof Part 1

Показать описание
In this video I go over the cycloid curve and derive the parametric equations for the case in which the angle inside the circle is between 0 and π/2. The cycloid is formed by tracing a point on the circumference of a circle as it rotates along a straight line. The resulting parametric equations are shown below:
x = r(θ - sinθ)
y = r(1 - cosθ)
Although I derived these equations for the case where θ is between 0 and π/2, these equations do in fact work for all values of θ. I will go over the proof for other values of θ in a later video so stay tuned for that!
Also, these parametric equations can be rearranged to eliminate θ and to write x as a function of y, but the resulting Cartesian equation is much more complicated. I will nonetheless derive the Cartesian form of the cycloid in a later video, as well as the very interesting history of the cycloid, so stay tuned!
Related Videos:
------------------------------------------------------
x = r(θ - sinθ)
y = r(1 - cosθ)
Although I derived these equations for the case where θ is between 0 and π/2, these equations do in fact work for all values of θ. I will go over the proof for other values of θ in a later video so stay tuned for that!
Also, these parametric equations can be rearranged to eliminate θ and to write x as a function of y, but the resulting Cartesian equation is much more complicated. I will nonetheless derive the Cartesian form of the cycloid in a later video, as well as the very interesting history of the cycloid, so stay tuned!
Related Videos:
------------------------------------------------------
Parametric Curves: Example 7: The Cycloid: Proof Part 1
Math 1A 1.7 Example 7 Deriving Parametric Equations for a Cycloid
Parametric Curves - 10.1.7
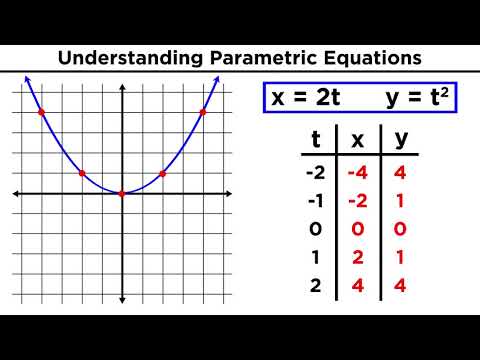
Examples of Parametric Curves
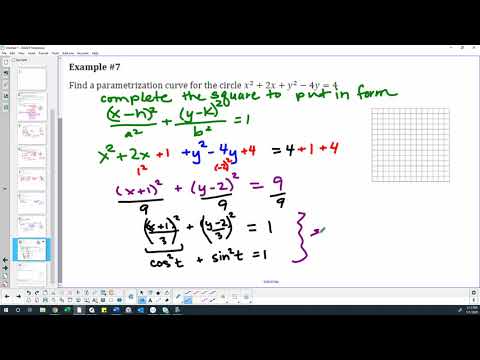
Plane Curves: Parametric Equations - 03 Example: Finding a Parametrization
Parametric Curves: Example 6: Graphing Devices
Precalculus 7-06 Parametric Equations
Parametric Equations
5th Fusion HPC Workshop - Day 2
Parametric Curves: Example 8: The Cycloid: Proof Part 2
Parametric Equations Introduction, Eliminating The Paremeter t, Graphing Plane Curves, Precalculus
Parametric Equations and Motion (Section 6.3)
Parametric Curves: History of The Cycloid
Multivariable Calculus - Lecture 1: Parametric Curves, and Calculus with Parametric Curves
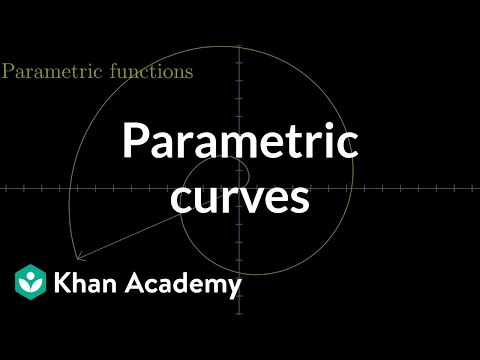
Parametric curves | Multivariable calculus | Khan Academy
Math 1060 SLCC 8.2 Video 6 example 7 find parametric equations
1.7 Parametric Curves
Tangent Lines of Parametric Curves
Calculus 2: Parametric Equations (7 of 20) How to Derive Parametric Equations Ex. 2
Parametric Curves: Example 11: Conchoids of Nicomedes
Math 1207-R03 Lecture 22 - Intro to Parametric Curves and Parametrization
Example of Parametric equations. Matching Graphs
Parametric Equations in 7 minutes
Section 11 7 Parametric Equations Example 1
Комментарии
 0:14:41
0:14:41
 0:06:25
0:06:25
 0:05:09
0:05:09
 0:20:08
0:20:08
 0:03:09
0:03:09
 0:09:31
0:09:31
 0:06:44
0:06:44
 0:04:36
0:04:36
 7:29:58
7:29:58
 0:14:50
0:14:50
 0:33:29
0:33:29
 0:11:19
0:11:19
 0:07:59
0:07:59
 1:08:39
1:08:39
 0:05:51
0:05:51
 0:07:35
0:07:35
 0:43:04
0:43:04
 0:13:55
0:13:55
 0:02:10
0:02:10
 0:13:24
0:13:24
 0:54:08
0:54:08
 0:09:56
0:09:56
 0:07:39
0:07:39
 0:01:17
0:01:17