filmov
tv
Trucos para Resolver Rápidamente Ecuaciones EXPONENCIALES

Показать описание
Para clases personalizadas o particulares conmigo directamente, así como asesorías, ayudas para tareas escolares, preparación para exámenes u otras ayudas, escribe al correo:
-----------------
Denis Solver Math.
En este video, resolveremos una ecuación exponencial utilizando los métodos de sustitución y logaritmos obteniendo la solución real y descartando las complejas. Exploraremos paso a paso cómo transformar una ecuación complicada en una más sencilla y manejable, y cómo los logaritmos nos ayudan a encontrar la solución exacta. Ideal para estudiantes de secundaria y universitarios, así como para cualquier persona interesada en profundizar su comprensión de las matemáticas. ¡No olvides suscribirte y activar la campanita para no perderte ningún nuevo contenido!
---------------------------
In this video, we'll solve an exponential equation using the substitution and logarithm methods. We'll explore step-by-step how to transform a complex equation into a simpler, more manageable one, and how logarithms help us find the exact solution. Ideal for high school and college students, as well as anyone interested in deepening their understanding of mathematics. Don't forget to subscribe and hit the bell to never miss out on new content!
------------------------------
Descarga gratuita de la lección en formato PDF:
---------------------------------
Se recomienda que seguidamente veas uno de estos videos:
------------------------------------------------
Conviértete en miembro de este canal para disfrutar de ventajas:
----------------------------------------------------
╔═╦╗╔╦═╦═╦╦╦╦╗╔═╦══╦═╗
║╚╣║║║╚╣╔╣╔╣║╚╣═╬╗╔╣═╣
╠╗║╚╝╠╗║╚╣║║║║║═╣║║║═╣
Si te gustó el vídeo, dale a "Me gusta", comenta y no olvides suscribirte y activar "Todas las notificaciones" 🔔
-------------------------
Capítulos del video:
00:00 INTRO
00:25 Intercambio de exponentes
01:07 Sustitución
01:33 Descomposición
02:34 Factorización
03:00 Diferencia de cuadrados
03:23 Factorización
03:40 Producto nulo
05:30 Devolución
05:40 Logaritmos
07:00 Comprobación
07:42 Gráfica
08:02 Ver video recomendado
08:26 Despedida
-----------------
Denis Solver Math.
En este video, resolveremos una ecuación exponencial utilizando los métodos de sustitución y logaritmos obteniendo la solución real y descartando las complejas. Exploraremos paso a paso cómo transformar una ecuación complicada en una más sencilla y manejable, y cómo los logaritmos nos ayudan a encontrar la solución exacta. Ideal para estudiantes de secundaria y universitarios, así como para cualquier persona interesada en profundizar su comprensión de las matemáticas. ¡No olvides suscribirte y activar la campanita para no perderte ningún nuevo contenido!
---------------------------
In this video, we'll solve an exponential equation using the substitution and logarithm methods. We'll explore step-by-step how to transform a complex equation into a simpler, more manageable one, and how logarithms help us find the exact solution. Ideal for high school and college students, as well as anyone interested in deepening their understanding of mathematics. Don't forget to subscribe and hit the bell to never miss out on new content!
------------------------------
Descarga gratuita de la lección en formato PDF:
---------------------------------
Se recomienda que seguidamente veas uno de estos videos:
------------------------------------------------
Conviértete en miembro de este canal para disfrutar de ventajas:
----------------------------------------------------
╔═╦╗╔╦═╦═╦╦╦╦╗╔═╦══╦═╗
║╚╣║║║╚╣╔╣╔╣║╚╣═╬╗╔╣═╣
╠╗║╚╝╠╗║╚╣║║║║║═╣║║║═╣
Si te gustó el vídeo, dale a "Me gusta", comenta y no olvides suscribirte y activar "Todas las notificaciones" 🔔
-------------------------
Capítulos del video:
00:00 INTRO
00:25 Intercambio de exponentes
01:07 Sustitución
01:33 Descomposición
02:34 Factorización
03:00 Diferencia de cuadrados
03:23 Factorización
03:40 Producto nulo
05:30 Devolución
05:40 Logaritmos
07:00 Comprobación
07:42 Gráfica
08:02 Ver video recomendado
08:26 Despedida
Комментарии
 0:08:34
0:08:34
 0:05:27
0:05:27
 0:00:47
0:00:47
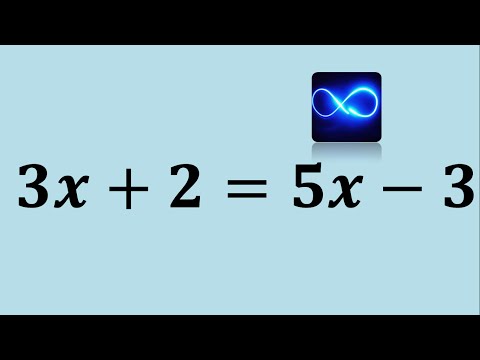 0:03:34
0:03:34
 0:09:42
0:09:42
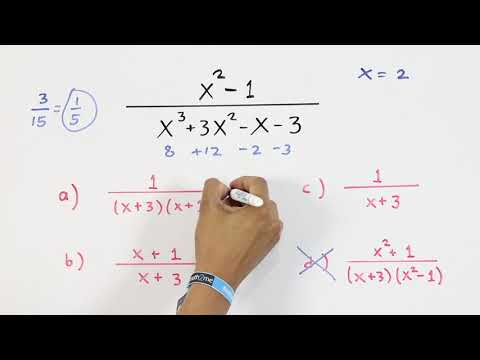 0:05:21
0:05:21
 1:32:56
1:32:56
 0:00:43
0:00:43
 0:12:26
0:12:26
 0:00:17
0:00:17
 0:09:22
0:09:22
 0:03:37
0:03:37
 0:24:23
0:24:23
 0:00:42
0:00:42
 0:11:13
0:11:13
 0:09:20
0:09:20
 0:03:44
0:03:44
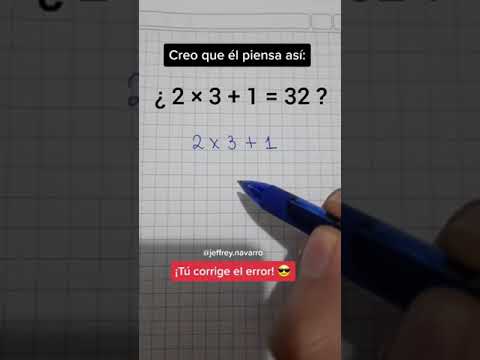 0:00:23
0:00:23
 0:07:42
0:07:42
 0:07:34
0:07:34
 0:06:29
0:06:29
 0:00:59
0:00:59
 0:04:55
0:04:55
 0:01:00
0:01:00