Easy how to hamming code for single error correction sec

hamming code for single error correction (sec): a detailed tutorial

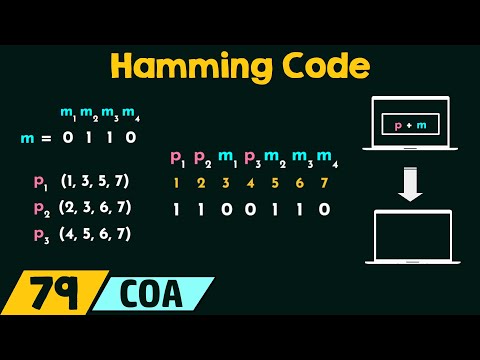
hamming code is a powerful error detection and correction code used in digital communication and storage systems. it's particularly effective for detecting and correcting *single-bit errors*, making it ideal for scenarios where errors are infrequent but critical. this tutorial will provide a step-by-step guide to understanding and implementing hamming code for single error correction (sec).

**1. understanding the core concepts**

* **data bits (d):** these are the actual bits of information you want to transmit or store (e.g., a byte representing a character).
* **redundancy bits (r):** these are extra bits added to the data bits. they contain parity information that allows you to detect and correct errors. these are also often called parity bits.
* **codeword:** the combination of data bits and redundancy bits. this is the actual sequence transmitted/stored.
* **parity:** parity refers to whether the number of 1s in a given set of bits is even or odd. even parity means an even number of 1s, while odd parity means an odd number of 1s. hamming code uses parity to detect errors.
* **error detection and correction:** hamming code's magic lies in how redundancy bits are placed and used. each redundancy bit checks the parity of a specific group of bits in the codeword. if an error occurs in one of these groups, the corresponding redundancy bit will indicate it. by analyzing which redundancy bits indicate an error, the exact location of the error can be identified, allowing for correction.

**2. determining the number of redundancy bits (r)**

the most crucial step is determining how many redundancy bits are needed for a given number of data bits. this is governed by the following inequality:

**2supr/sup ≥ d + r + 1**

where:

* `r` is the number of redundancy bits.
* `d` is the number of data bits.

the formula basically states that the number of possible states that the redundan ...

#HammingCode #ErrorCorrection #php
Hamming code
single error correction
error detection
coding theory
data transmission
information theory
parity bits
error correction codes
binary codes
Hamming distance
data integrity
digital communication
coding techniques
redundancy
data reliability