implicit differentiation with square roots

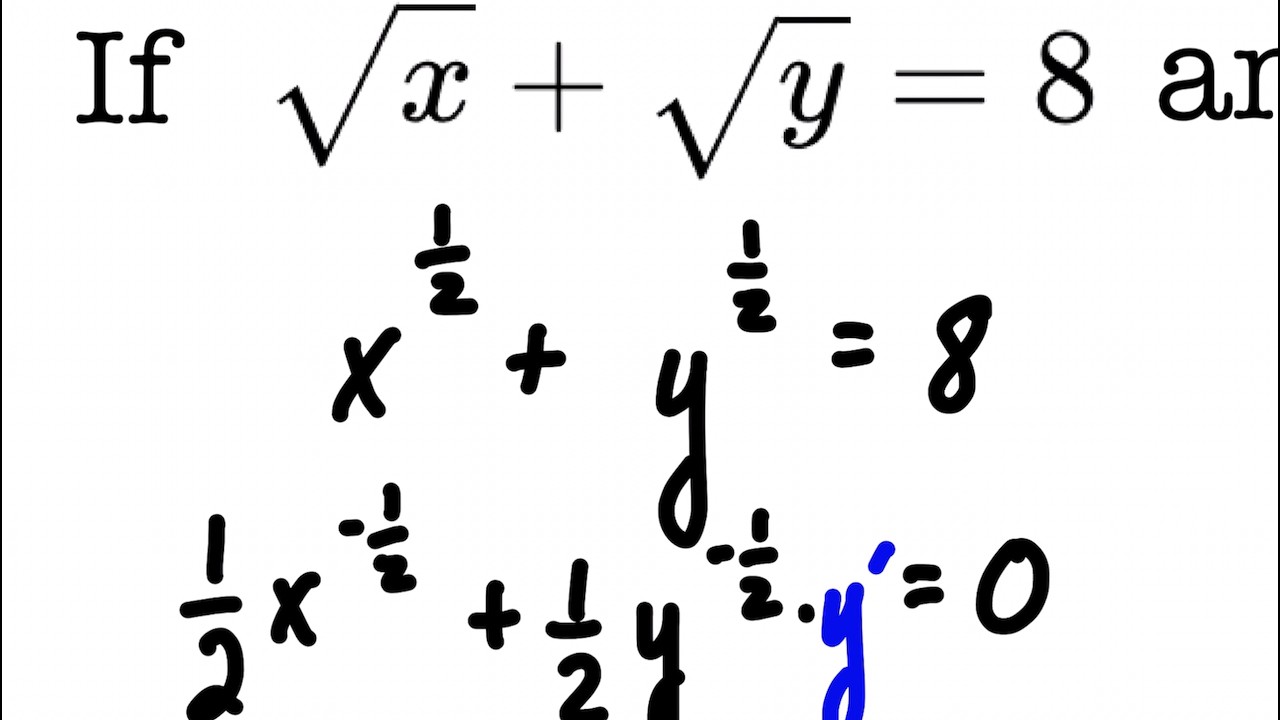
preview_player
Показать описание
In this math example, we are given an equation that contains two variables, both under square roots. We find the derivative, y' = dy/dx, and evaluate it at a given point by using implicit differentiation. Each step of this process is gone through and explained as we use the power rule to take our derivatives, then rearrange the equation to isolate y' on one side by itself. Because of the square roots, we rewrite them as fractional exponents and use the power rule, that makes us end up with negative exponents. These are rewritten as positive when simplifying.

sqrt(x)+sqrt(y)=
  1. Math Tutorials
Рекомендации по теме
Implicit Differentiation With 0:07:22

Implicit Differentiation With Square Root

How to use 0:01:29

How to use implicit differentiation with the square root for chain and product rule

Implicit Differentiation of 0:09:09

Implicit Differentiation of sqrt(xy) = x^2y+1 ❖ Calculus

Calculus - Implicit 0:04:25

Calculus - Implicit Differentiation example (Request)

sqrt(x+y) = x 0:01:51

sqrt(x+y) = x Implicit Differentiation find dy/dx

Implicit Differentiation with 0:03:16

Implicit Differentiation with Square Roots

Understand Implicit differentiations 0:07:02

Understand Implicit differentiations of square root functions

implicit differentiation with 0:06:28

implicit differentiation with square roots

Advancing Calculus Research 1:24:32

Advancing Calculus Research and Teaching with Wolfram Language

Implicit Derivation x^(1/2) 0:03:06

Implicit Derivation x^(1/2) + y^(1/2) = 1 Sum of Square roots

Derivatives of Radical 0:15:30

Derivatives of Radical Functions

🍅👥👤🧰Amended video for 0:01:54

🍅👥👤🧰Amended video for implicit differentiation with square roots:

Find second derivative 0:05:59

Find second derivative implicitly with respect to x for sqrt(x) + sqrt(y) = 1

Calculus Help: Implicit 0:03:04

Calculus Help: Implicit Differentiation: xy + sqrt(x+y)=21 - Techniques

Find derivative implicitly 0:07:13

Find derivative implicitly with respect to x for sqrt(xy) = 1 + x^2 y

🍅👥Calculus Implicit differentiation 0:26:04

🍅👥Calculus Implicit differentiation with square roots: Text 559-744-3169 for services!

How to use 0:01:38

How to use the chain rule with a square root

Find derivative implicitly 0:05:39

Find derivative implicitly with respect to x for sqrt(x +y) = 1 + x^2 y^2

Second Derivative of 0:02:51

Second Derivative of Square Roots

Find dy/dx by 0:17:50

Find dy/dx by implicit differentiation | sqrt(x + y) = x^4 + y^4

Chain rule with 0:01:36

Chain rule with radicals, how to take the derivative

The Quotient Rule 0:07:39

The Quotient Rule - Example 2

Using power rule 0:02:20

Using power rule with square root to take derivative on a logarithm

Taking the derivative 0:02:07

Taking the derivative with a square root and tangent

Комментарии
Автор

I can actually see how powerful this implicit differentiation technique is when you apply it to related rates of change

OSAS
Автор

You just simply find a formula that relates all of the values that you’re either trying to differentiate or not, and you simply differentiate that formula and then solve for the differential you are looking for.

OSAS