filmov
tv
Derivatives of Radical Functions

Показать описание
This calculus video tutorial explains how to find the derivative of radical functions using the power rule and chain rule for derivatives. It explains how to find the derivative of square root functions and cube root functions.
Derivatives - Fast Review:
Equation of the Tangent Line:
Derivatives - Horizontal Tangent Line:
The Equation of The Normal Line:
The Equation of The Secant Line:
_________________________________
Average and Instantaneous Velocity:
Instantaneous Rate of Change:
Derivatives of Rational Functions:
Derivatives of Radical Functions:
Derivatives of Fractions:
________________________________
Derivatives - Higher Order:
Simplifying Derivatives:
Derivatives - The Product Rule:
Derivatives - The Quotient Rule:
Derivatives - The Chain Rule:
_______________________________________
Final Exams and Video Playlists:
Full-Length Videos and Worksheets:
Derivatives - Formula Sheet:
Derivatives - Fast Review:
Equation of the Tangent Line:
Derivatives - Horizontal Tangent Line:
The Equation of The Normal Line:
The Equation of The Secant Line:
_________________________________
Average and Instantaneous Velocity:
Instantaneous Rate of Change:
Derivatives of Rational Functions:
Derivatives of Radical Functions:
Derivatives of Fractions:
________________________________
Derivatives - Higher Order:
Simplifying Derivatives:
Derivatives - The Product Rule:
Derivatives - The Quotient Rule:
Derivatives - The Chain Rule:
_______________________________________
Final Exams and Video Playlists:
Full-Length Videos and Worksheets:
Derivatives - Formula Sheet:
Комментарии
 0:15:30
0:15:30
 0:05:54
0:05:54
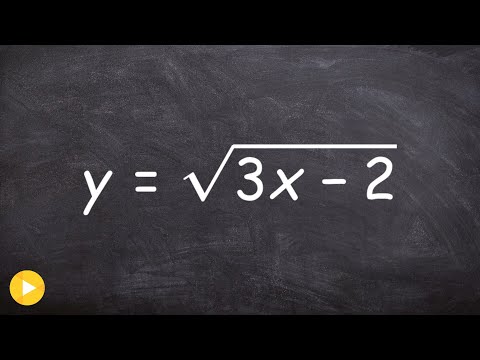 0:01:36
0:01:36
 0:11:04
0:11:04
 0:10:24
0:10:24
 0:02:39
0:02:39
 0:05:09
0:05:09
 0:11:12
0:11:12
 0:07:34
0:07:34
 0:01:45
0:01:45
 0:03:59
0:03:59
 0:00:22
0:00:22
 0:01:38
0:01:38
 0:07:39
0:07:39
 0:09:14
0:09:14
 0:05:58
0:05:58
 0:02:02
0:02:02
 0:52:51
0:52:51
 0:06:04
0:06:04
 0:05:28
0:05:28
 0:05:22
0:05:22
 0:18:40
0:18:40
 0:06:33
0:06:33
 0:06:29
0:06:29