Partially Ordered Sets and Hasse Diagrams | Discrete Math

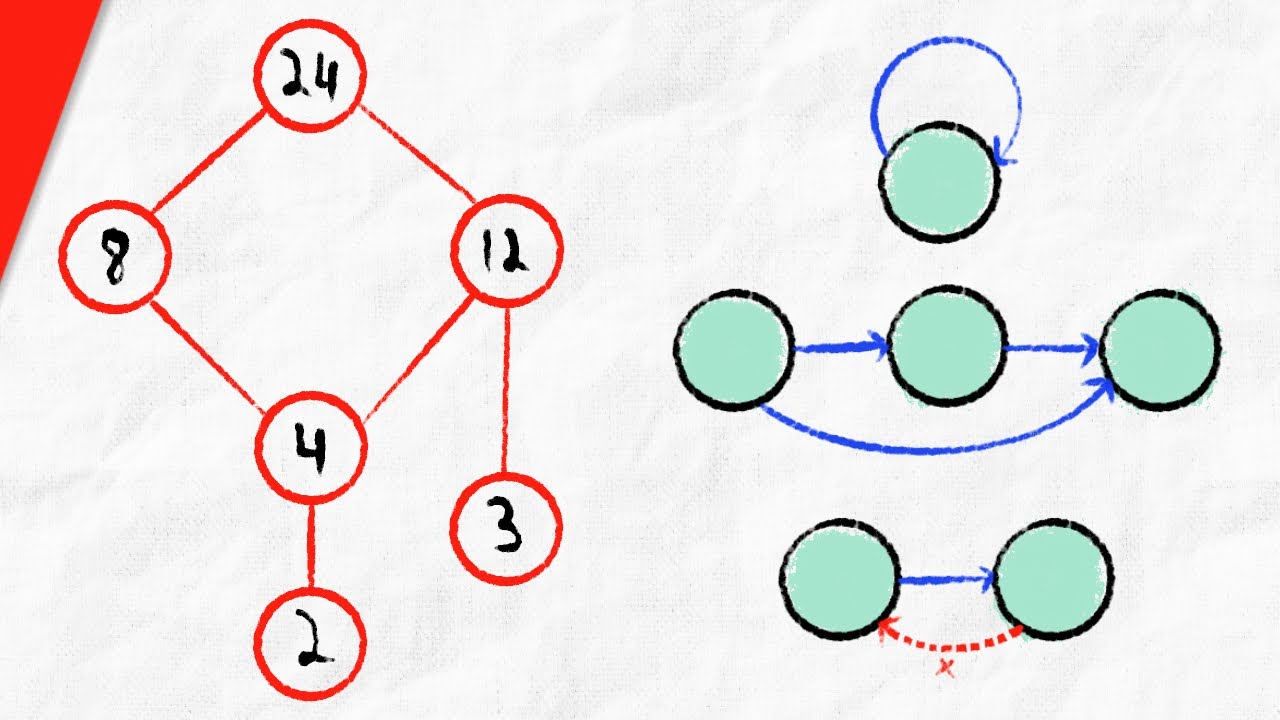
We cover posets (partially ordered sets) and Hasse diagrams that represent them. We'll see examples of sets with partial orders on them, beginning with a power set and the subset relation. Partial orders are reflexive, transitive, and antisymmetric, which we discuss with examples. We also cover the construction of Hasse diagrams, as well as minimal, maximal, minimum, and maximum elements of a partially ordered set. #discretemathematics

◉Textbooks I Like◉

★DONATE★

Thanks to Petar, dric, Rolf Waefler, Robert Rennie, Barbara Sharrock, Joshua Gray, Karl Kristiansen, Katy, Mohamad Nossier, and Shadow Master for their generous support on Patreon!

Follow Wrath of Math on...

[shayanzaidi]

Getting through discrete maths without a teacher is an absolute nightmare. I'm so glad I found your channel!!

[Xorked]

Honestly the best math channel I've seen for Discrete Mathematics, great work

[anesp.a]

Honestly You are a Lion in Discrete Mathematics... From Kerala, India .. Keep it up Sir

[Eggtamaa]

man this 16 minute video covered so much. thank you and please continue making videos!

[myronparaskevopoulos]

🎯 Key Takeaways for quick navigation:

00:27 📚 *A partially ordered set (poset) is defined by a relation that is reflexive, anti-symmetric, and transitive.*
02:48 🛠️ *The power set of a set, with the subset relation as the partial order, forms a poset.*
05:42 🔄 *Hasse diagrams visually represent posets without the need for arrows by ensuring a consistent direction of the relation.*
11:53 📈 *Maximal elements in a poset relate only to themselves and can be found at the tops of components in a Hasse diagram.*
13:24 📉 *Minimal elements in a poset relate only to themselves and can be found at the bottoms of components in a Hasse diagram.*

Made with HARPA AI

[AManWithaZ]

This video is a really great break-down on the fundamentals. PO sets and Hasse Diagrams have recently been on my mind because I've been trying to teach myself a subject involving filters and ultrafilters, and Hasse Diagrams are a great way to visualize them.

[jingyiwang]

I am really grateful for your patient and detailed explanation. This has helped me a lot as I am previewing for my discrete mathematics class for the coming fall semester. And I think that your videos are among the best discrete mathematics tutorial. I can watch your videos regularly as I proceed with my next semester as well. Thank you so much!

[ea]

This is my go to guy for discrete maths.

[priya-fzpj]

He is the best.. every time i have a doubt..there is never a chance it's not cleared by watching his videos..keep up the good work

[punditgi]

Nothing partial about the quality of this lesson!

[musicheals]

Thank you so much sir
I was preparing for my entrance exam, and I got your video which was very easy to understand

[joanofarc]

Thank you so much! Clear and informative!

[Leo-nglq]

I dont even speak english that well, and yet i could understand every single thing. Thanks!!

[DrunkenJanitor]

Great Video Helped out a lot, Thankyou!

[nadred]

this guy is literally jesus himself re-incarnated as the math god, all hail Shawn

[roblox]

Do you have a course playlist for Discrete Math?

[seven-rz]

Is the "maximun" and "minimum" the same as "upper bound" and "lower bound" respectively?

[the.graduate]

You earned one more suscription by this vid!❤ love you to

[Liichess]

thanks so much exam is some min away thanks

[rtxa]

Very nice video but I miss that you didn't talk about upper and lower bound :(