filmov
tv
Limit tanx-sinx/x^3 as x approaches 0 (without L'Hopital's rule)
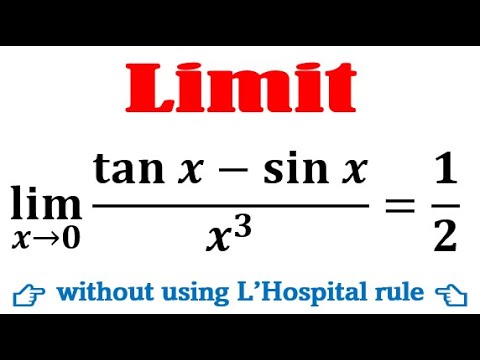
Показать описание
#limit
lim x-0 (tanx-sinx)/x^3 =1/2
Find the limit of tanx-sinx/x3 as x approaches 0 without using the L'Hospital's (L'Hopital's) rule.
Welcome to join 🤗
Feel free to raise/ask questions.
lim x-0 (tanx-sinx)/x^3 =1/2
Find the limit of tanx-sinx/x3 as x approaches 0 without using the L'Hospital's (L'Hopital's) rule.
Welcome to join 🤗
Feel free to raise/ask questions.
Limit tanx-sinx/x^3 as x approaches 0 (without L'Hopital's rule)
limit tanx-sinx/x^3 as x approaches 0
Limit of (tan x - sin x)/x^3 as x approaches 0
Limits of Trigonometric Functions
limx→0(tanx-sinx)/x^3=?
Why the limit tanx-sinx/x3 is not 0?
Evaluate: lim_(xrarr0) (tan x-sin x)/(x^(3)) | 11 | LIMITS AND DERIVATIVES | MATHS | NAGEEN PRA...
limit of 3x/tan(x)) as x goes to 0 ( limits of trigonometric functions )
I Tried Learning Calculus In One Hour #JEEMAINS2025
limit x tends to zero (tanx-sinx)/x^3
Limit tanx-sinx/x3 when x approaches 0
Limit of (tanx-sinx)/x^3 as x approaches 0
Important Trig Limit with (tanx-sinx)/sin^3x
Limit (tanx - sinx)/(sinx)^3 as x approaches to zero Proof |Mad Teacher
lim x→0( tanx-sinx/x^3) || L'Hospital Rule
Limit as x approaches 0 y = sin^3x/(sinx-tanx)
limit x - 0 (tan x - sin x)/(x^3) ...
The value of `lim_(xrarr0)(tanx-sinx)/(x^3)`, is
How REAL Men Integrate Functions
`lim_(x- gt0) (tan x - sin x)/(x^3)` is equal to
And You Thought Trigonometry Was Pointless…
Evaluate: `lim_(x- gt0) (sinx-tanx)/x^3`
Limit of x-sinx/x^3 as x approaches 0
Evaluate: lim_(x ~0)(tanx-sin x)/(x^(3))
Комментарии
 0:04:14
0:04:14
 0:04:15
0:04:15
 0:15:23
0:15:23
 0:02:51
0:02:51
 0:02:44
0:02:44
 0:03:08
0:03:08
 0:01:48
0:01:48
 1:06:56
1:06:56
 0:06:04
0:06:04
 0:02:45
0:02:45
 0:04:25
0:04:25
 0:04:15
0:04:15
 0:04:43
0:04:43
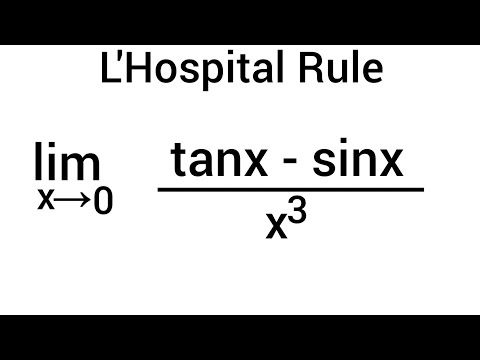 0:03:04
0:03:04
 0:04:36
0:04:36
 0:04:02
0:04:02
 0:02:32
0:02:32
 0:00:35
0:00:35
 0:02:01
0:02:01
 0:01:00
0:01:00
 0:01:50
0:01:50
 0:01:35
0:01:35
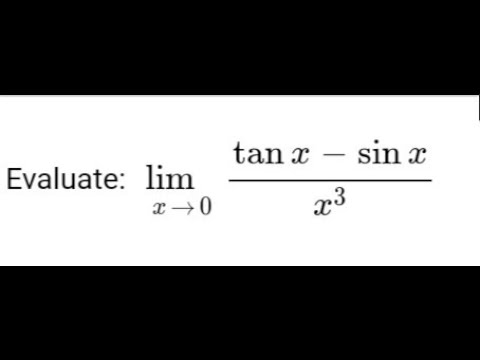 0:06:59
0:06:59