filmov
tv
Periodic trajectories in a Tokarsky room

Показать описание
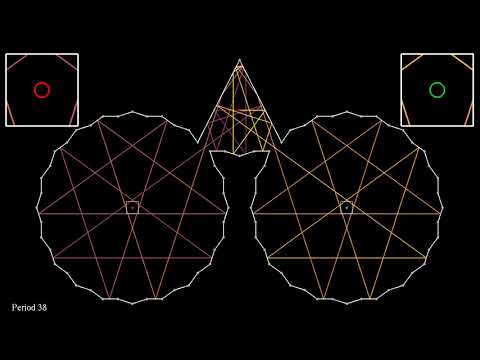
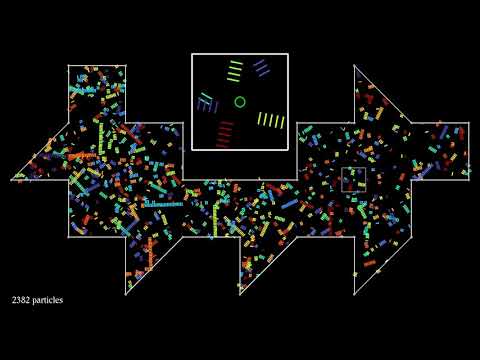
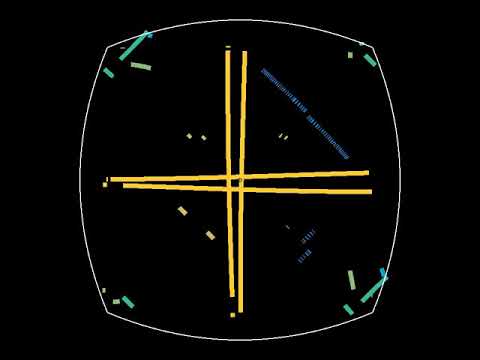
In this simulation, a single trajectory starts on the vertical symmetry axis of the room, in a horizontal direction. The trajectory is reflected on the sides of the room, and absorbed whenever it reaches a corner. The color changes slightly after each reflection. One can see that whenever the trajectory is not absorbed, it loops back to its starting point. The period of the looping trajectory (that is, the number of bounces before returning to the starting point) is shown at the bottom left. This looping behavior is due to the fact that the trajectory can only take a finite number of directions, because all angles involved are multiples of 9°.
The illumination problem asks the following question: assume you have a room with mirrored walls. Is it always possible to place a light source in such a way that no dark corners remain in the room? Of course, the room has to be "in one piece" (connected, as we say in mathematics): it should not consist of several separate rooms.
A second example, containing only straight walls, was found by Tokarsky in 1995. The solution works in the approximation of geometric optics, meaning that light travels in straight lines. Unlike Penrose's solution, it leaves only one single point in the dark, provided one considers that any ray hitting a vertex of the polygon disappears. The same holds for the room shown here.
Render time: 1 minute
Color scheme: Plasma by Nathaniel J. Smith, Stefan van der Walt and Eric Firing
Some outreach articles on mathematics:
(in French, some with a Spanish translation)
The illumination problem asks the following question: assume you have a room with mirrored walls. Is it always possible to place a light source in such a way that no dark corners remain in the room? Of course, the room has to be "in one piece" (connected, as we say in mathematics): it should not consist of several separate rooms.
A second example, containing only straight walls, was found by Tokarsky in 1995. The solution works in the approximation of geometric optics, meaning that light travels in straight lines. Unlike Penrose's solution, it leaves only one single point in the dark, provided one considers that any ray hitting a vertex of the polygon disappears. The same holds for the room shown here.
Render time: 1 minute
Color scheme: Plasma by Nathaniel J. Smith, Stefan van der Walt and Eric Firing
Some outreach articles on mathematics:
(in French, some with a Spanish translation)
Комментарии
 0:01:25
0:01:25
 0:03:21
0:03:21
 0:01:21
0:01:21
 0:06:01
0:06:01
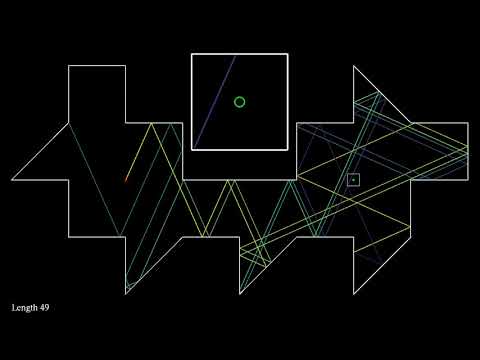 0:08:53
0:08:53
 0:00:47
0:00:47
 0:03:21
0:03:21
 0:02:01
0:02:01
 0:02:05
0:02:05
 0:04:53
0:04:53
 0:00:58
0:00:58
 0:04:03
0:04:03
 0:03:03
0:03:03
 0:02:59
0:02:59
 0:01:41
0:01:41
 0:01:22
0:01:22
 0:03:47
0:03:47
 0:18:45
0:18:45
 1:02:49
1:02:49
 0:01:05
0:01:05
 0:00:55
0:00:55
 0:02:01
0:02:01
![[Epilepsy warning] Trajectory](https://i.ytimg.com/vi/Xa0lZLIGlPU/hqdefault.jpg) 0:06:05
0:06:05
 0:02:45
0:02:45