filmov
tv
Limit at infinity
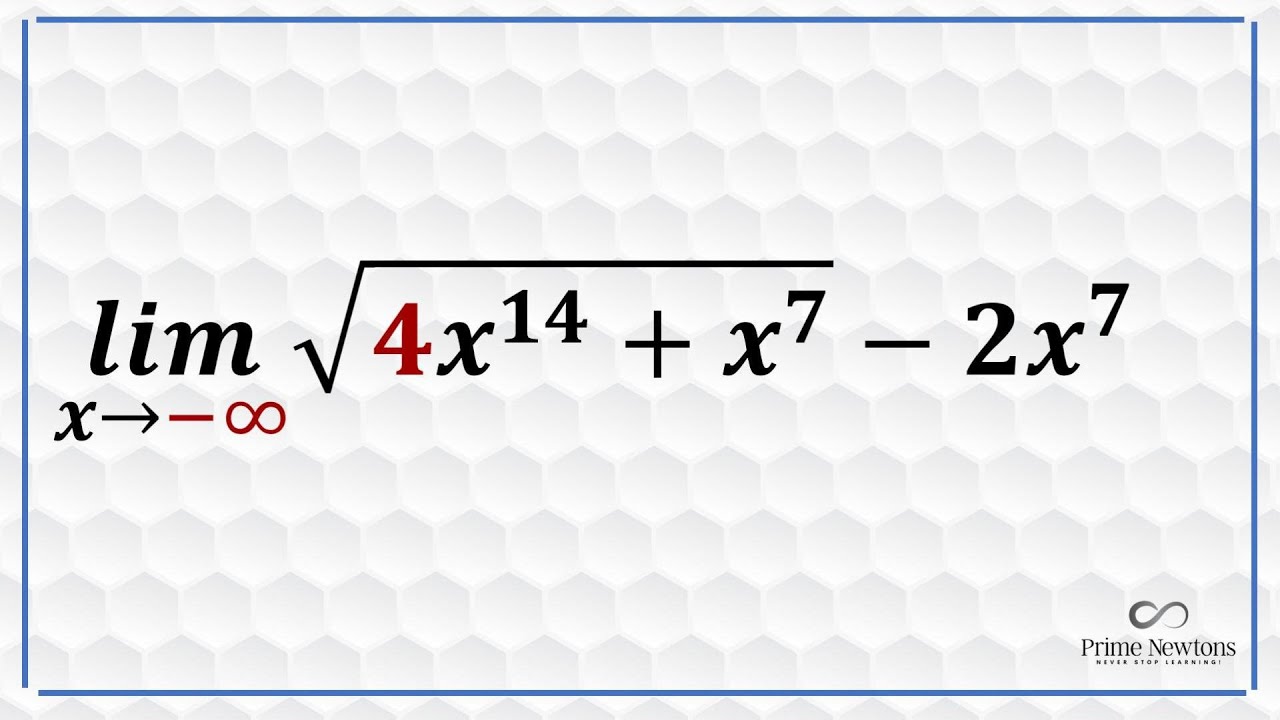
Показать описание
In this video, I showed how to evaluate a survd limit at negative infinity
How To Find The Limit At Infinity
Infinite Limit Shortcut!! (Calculus)
Limits at Infinity & Horizontal Asymptotes
Learn how to evaluate a limit at infinity
Limit solving (limit at infinity of a rational function)
How to Find the Limit at Infinity (NancyPi)
Limits at Infinity of Exponential Functions | How to find limits at infinity | Calculus - Part 4
Limits at Infinity (Rational square-root function as x approaches negative Infinity)
How to Calculate the Limit at Infinity in 1 minute? #maths #calculus #calculusmadeeasy #limits
Limits at Infinity
Limits at Infinity
Limit at infinity
Introduction to limits at infinity | Limits and continuity | AP Calculus AB | Khan Academy
Calculus 1 Lecture 3.5: Limits of Functions at Infinity
epsilon-N definition for a limit at infinity (introduction & how to write the proof)
Limits at infinity
FINDING THE LIMITS AT INFINITY | PART 1 | PROF D
Limits at infinity of quotients (Part 1) | Limits and continuity | AP Calculus AB | Khan Academy
Infinite Limits and Vertical Asymptotes
PreCalculus | Limits at Infinity
Infinite limits intro | Limits and continuity | AP Calculus AB | Khan Academy
Solving Limits Mentally #calculus #limit #infinity #rational
SHORTCUT TO LIMIT TO INFINITY ♾️
Limit at infinity of exponential function
Комментарии
 0:13:14
0:13:14
 0:00:51
0:00:51
 0:19:24
0:19:24
 0:01:40
0:01:40
 0:01:00
0:01:00
 0:30:49
0:30:49
 0:16:35
0:16:35
 0:09:52
0:09:52
 0:00:56
0:00:56
 0:09:54
0:09:54
 0:11:04
0:11:04
 0:13:35
0:13:35
 0:02:46
0:02:46
 1:23:49
1:23:49
 0:18:28
0:18:28
 0:03:58
0:03:58
 0:12:30
0:12:30
 0:04:07
0:04:07
 0:29:04
0:29:04
 0:11:44
0:11:44
 0:07:41
0:07:41
 0:01:00
0:01:00
 0:00:55
0:00:55
 0:12:01
0:12:01