Counting Integer Points in Polygons with Negative Numbers | A 'moral' Intro to Generating Functions

Turn on the subtitles for the BEST experience. :)

0:00 - Introduction
5:17 - Section 1: The What and Why of Generating Functions
15:18 - Section 2: Finding GFs for Lattice Counting Functions
34:11 - Section 3: Substituting Negative Numbers
47:46 - Section 4: The Finale
58:09 - Conclusion

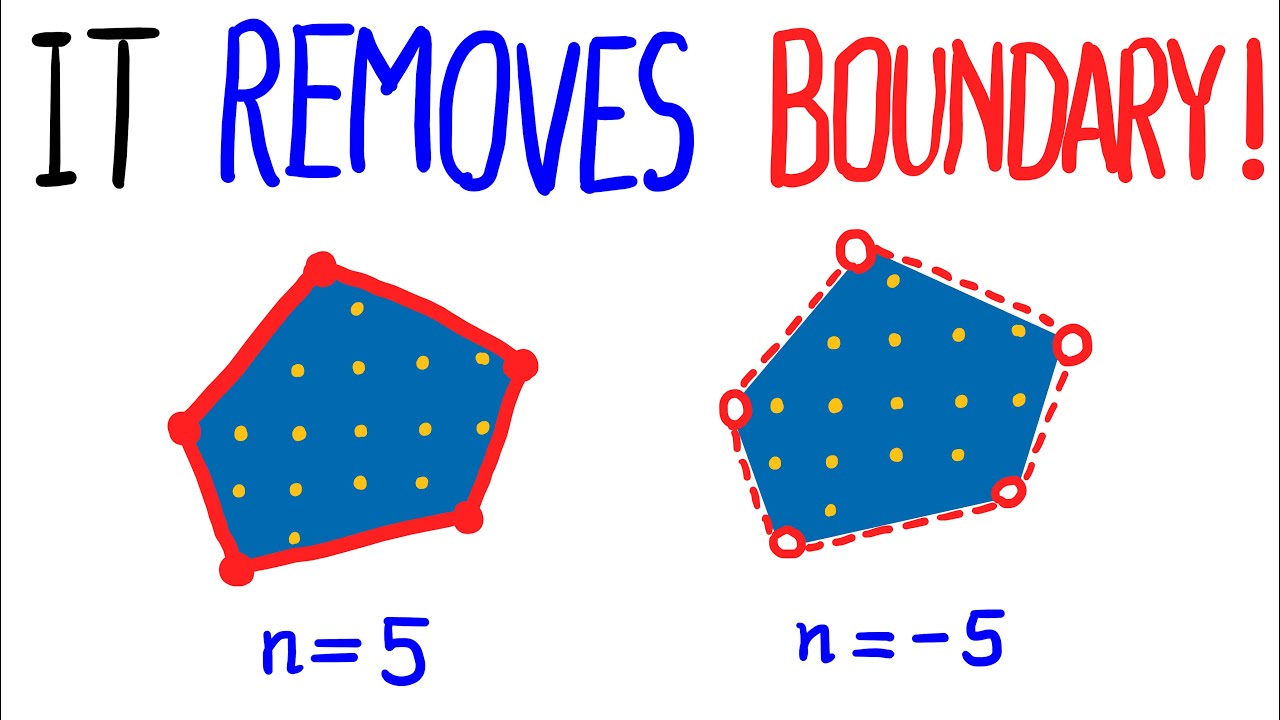
I tried my best to motivate generating functions and give an insight to why the generating functions work the way they should. Why they are intimately connected to the structure of the objects we are counting and their relation with linear homogenous recurrence relations is explained. The ideas are illustrated along the lines of the proof of the Ehrhart polynomials and Ehrhart Macdonald reciprocity which is about counting lattice points in dilated polytopes and what exactly are “negative dilates”. Making this video has been in the back of my mind for a while. Thank you so much to Grant and James for hosting Summer of Math Exposition 2 which helped me with my motivation to put this video together. :)

Sorry that I skipped over many details for the video. Please comment the plot holes that you find. If you want a non-hand-wavy version, or if you are interested to know more about reciprocity nature in combinatorics, give this book a read (at least the first chapter, highly recommended):

Music in this video

Stock footage credit to

#generatingfunctions #recurrence #SoME2

[pawebielinski]

Just after rewatch, I cannot fully exress how much I lika and appreciate this video.

[lexinwonderland]

This was absolutely fantastic! I can't wait to see more of your content!

[ArtArtisian]

I really appreciate the details being worked in time-lapse. It's a good touch.

[columbusmyhw]

Woah I _just_ learned about this (and by "just" I mean "a few weeks ago")! That timing is crazy!

[kohwenxu]

For those who might think the function f(n) at 14:09 is weird, that is the Fibonacci numbers in an explicit formula. The n in the formula must be an integer to see the Fibonacci numbers.

[azimuth]

Only 15 min in and this is extremely cool, thank you for making this video!!!

[rafiihsanalfathin]

Cute animation and overall enjoyable video! Even thought im not really familiar with this kind of mathematics but i can follow it pretty well. Nice submission!

[helloiamenergyman]

Hoo boy, I'll have an extremely enjoyable hour today :)

[horacehung]

The thumbnail can be more clickbaity :) Appreciate the 1-hour video effort. Impressive!

[columbusmyhw]

30:30 Why a _quadratic_ of z? Wouldn't it be a cubic? EDIT: Oh, right, you don't count the top vertex of the parallelopiped

[PhilipSmolen]

Are generating functions a new idea? I watch a lot of math, and I don't remember seeing this until recently.

[archieeliot]

Can I ask the shorcut formula how to solve 5 or more circles venn diagram😇😇Plsss help Thank you😇!