Marco Robalo (Paris): Gluing Invariants of Donaldson-Thomas Type

This talk was part of the workshop "Motivic and non-commutative aspects of enumerative geometry" held in July 2023 at Radboud University, Nijmegen, The Netherlands.

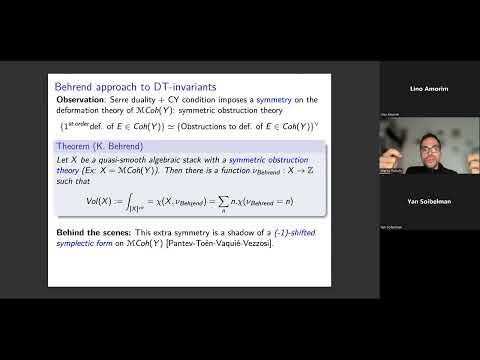
Abstract: We will explain how categorified Donaldson–Thomas invariants of Calabi–Yau 3-folds can be obtained by gluing singularity invariants from local models of a suitable moduli space endowed with a (-1)-shifted symplectic structure. We will show how to recover Brav–Bussi–Dupont–Joyce–Szendroi’s perverse sheaf categorifying the DT-invariants, as well as how to glue more evolved singularity invariants, such as matrix factorizations (thus answering a conjecture of Kontsevich and Soibelman). This is joint work with B. Hennion and J. Holstein.