filmov
tv
Projectile Motion: A Vector Calculus Problem
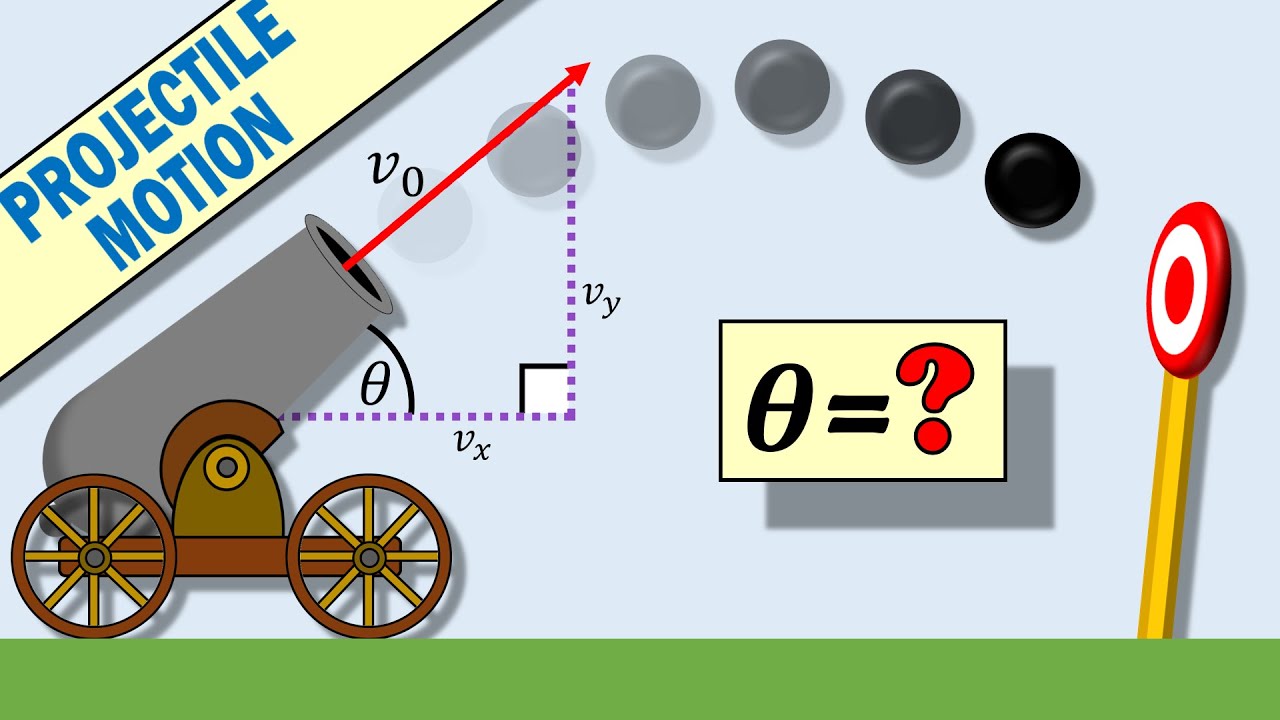
Показать описание
Projectile Motion: A Vector Calculus Problem
Vector Calculus Projectile Motion Calculating Launch Angle
Calculus 3: Vector Calculus: Motion in Plane (7 of 17) Projectile Motion Example
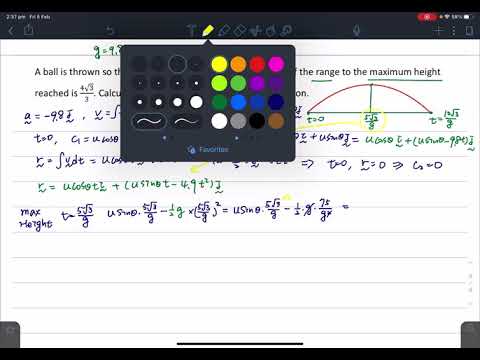
Projectile Motion using Vector Calculus
Kinematics Part 3: Projectile Motion
Calculus 3: Vector Calculus: Motion in Plane (6 of 15) Projectile Motion
Projectile Motion | Vector Calculus Math Lesson
Projectile motion | Vector calculus | Year 12 Specialist Maths
Calc 3 - 2.4.2 - Ideal Projectile Motion
Introduction to Projectile Motion - Formulas and Equations
Projectile motion Q1 | Vector calculus | Year 12 Specialist Maths
Projectile motion Q1 | Vector Calculus | Year 12 Specialist Maths
Position and velocity vectors in projectile motion (calculus based physics).
Projectile motion: The Equations (Acceleration, Velocity, Displacement)
Projectile motion | Vector Calculus |Year 12 Specialist Maths
Projectile Motion In Vector Form
Projectile motion - prof. Walter Lewin #shorts
How To Solve Any Projectile Motion Problem (The Toolbox Method)
Projectile Motion: 3 methods to answer ALL questions!
Projectile motion Q2 | Vector calculus | Year 12 Specialist Maths
Projectiles involving vectors
9.7-2 - Integrals and Projectile Motion
Projectile motion Q3 | Vector Calculus | Year 12 Specialist Maths
Projectile motion Q3 | Vector calculus | Year 12 Specialist Maths
Комментарии
 0:07:32
0:07:32
 0:07:26
0:07:26
 0:11:51
0:11:51
 0:13:44
0:13:44
 0:07:06
0:07:06
 0:03:20
0:03:20
 0:35:07
0:35:07
 0:09:43
0:09:43
 0:04:01
0:04:01
 0:28:11
0:28:11
 0:10:57
0:10:57
 0:10:57
0:10:57
 0:07:29
0:07:29
 0:11:55
0:11:55
 0:09:43
0:09:43
 0:04:02
0:04:02
 0:00:59
0:00:59
 0:13:02
0:13:02
 0:15:37
0:15:37
 0:13:30
0:13:30
 0:12:03
0:12:03
 0:04:52
0:04:52
 0:23:41
0:23:41
 0:23:41
0:23:41