filmov
tv
Find area of a quadrilateral in a very simple way.
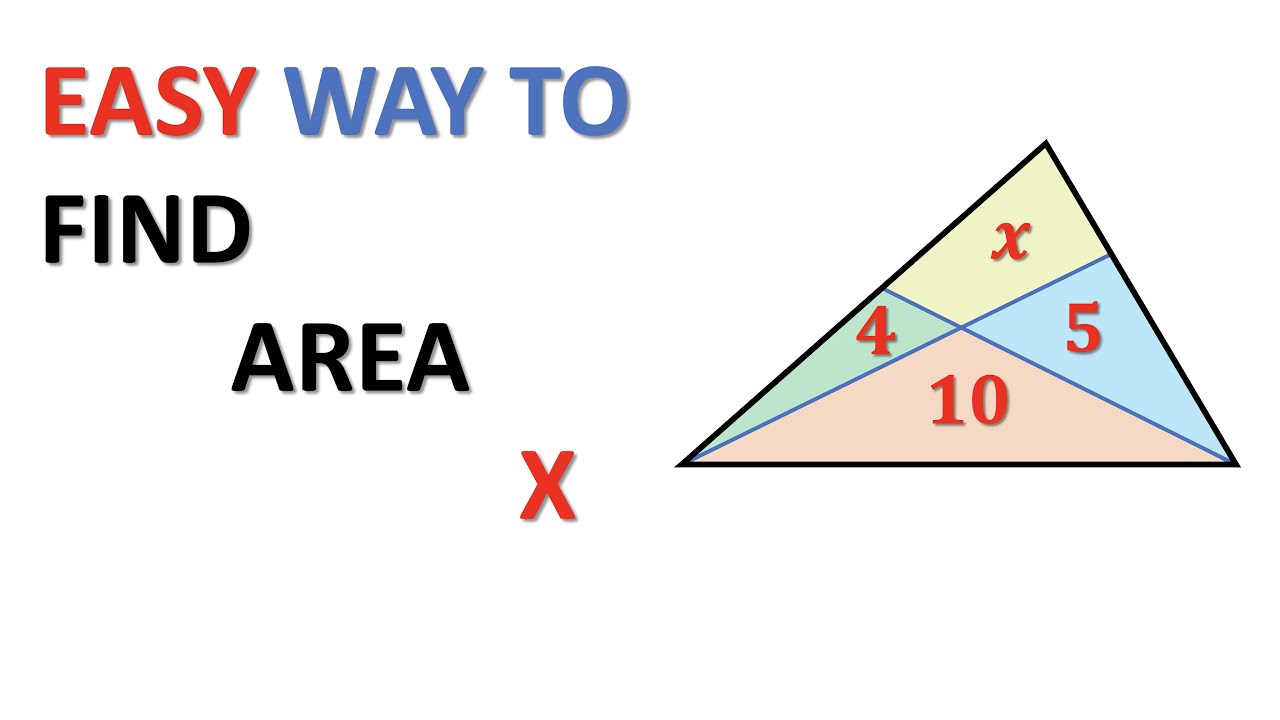
Показать описание
I have seen similar problems solved with fancy theorems. Nothing like that is needed!
How to find the area of a strange quadrilateral on a grid | Geometry | 6th grade | Khan Academy
Find the Area of a Quadrilateral on the Coordinate Plane
Find the area of the quadrilateral
Area of a Quadrilateral
Math Antics - Area
Area of a Rectangle, Triangle, Circle & Sector, Trapezoid, Square, Parallelogram, Rhombus, Geome...
Area of Quadrilateral || MATHS FORMULA
Find area of a quadrilateral in a very simple way.
Class 9th EM MATHS Circle
Quadrilaterals - Geometry
Quadrilateral Area Formulas.
Math Antics - Quadrilaterals
How To Find The Area Of Any Quadrilateral - Case 2 Part 1
How to Find Area of Quadrilateral
#quadrilateral | perimeter of quadrilateral | area of quadrilateral #maths
Area of a quadrilateral 4 points form
Find the Area of the Quadrilateral Given the Area of a Triangle
Area of Quadrilaterals
Area of a Quadrilateral
How to Find the Area of a Quadrilateral Given Three Sides & Two Included A... : Essential Math T...
How to Find Area of a Simple Quadrilateral / What is area of a quadrilateral formula
Finding the area of a quadrilateral
Area of quadrilateral with 2 parallel sides
How to find the area of Quadrilateral.
Комментарии
 0:03:54
0:03:54
 0:06:18
0:06:18
 0:09:52
0:09:52
 0:05:14
0:05:14
 0:10:26
0:10:26
 0:20:35
0:20:35
 0:00:21
0:00:21
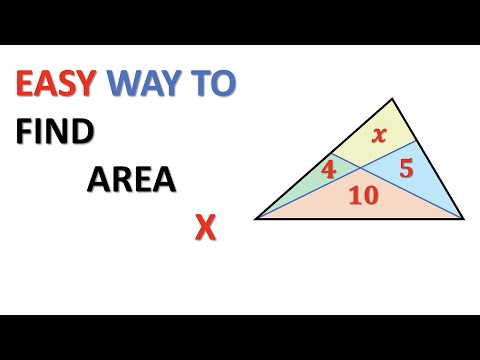 0:04:53
0:04:53
 0:20:28
0:20:28
 0:21:46
0:21:46
 0:00:08
0:00:08
 0:09:50
0:09:50
 0:09:31
0:09:31
 0:06:49
0:06:49
 0:00:36
0:00:36
 0:01:00
0:01:00
 0:03:31
0:03:31
 0:03:53
0:03:53
 0:03:18
0:03:18
 0:02:59
0:02:59
 0:03:45
0:03:45
 0:08:21
0:08:21
 0:03:42
0:03:42
 0:05:48
0:05:48