Lecture 23: The Dirichlet Problem on an Interval

preview_player
Показать описание
MIT 18.102 Introduction to Functional Analysis, Spring 2021
Instructor: Dr. Casey Rodriguez

We conclude this course on functional analysis by applying our understanding of the material to the well-posedness theory for the Dirichlet problem on an interval.

License: Creative Commons BY-NC-SA

  1. MIT OpenCourseWare
  2. Dirichlet problem
  3. Dirichlet problem on an interval
Рекомендации по теме
Lecture 23: The 1:23:54

Lecture 23: The Dirichlet Problem on an Interval

Lecture 23: The 0:59:22

Lecture 23: The Dirichlet Problem for Laplace's equation on discs

Lecture 23 (Solving 0:43:11

Lecture 23 (Solving the Heat Equation with Dirichlet and Neumann conditions)

Solve the Dirichlet 0:15:40

Solve the Dirichlet problem of the Laplace equation in a domain Ω

PDE. Lecture #23. 0:54:07

PDE. Lecture #23. Green’s Function for a ball. Poisson’s integral formula. Harnack's inequality...

Lecture 24 Solution 0:59:32

Lecture 24 Solution of the Dirichlet's Problem

Lecture 23 Dirichlet 1:20:51

Lecture 23 Dirichlet Processes

Example of a 0:03:35

Example of a Dirichlet problem

59.2 The Dirichlet 0:34:42

59.2 The Dirichlet Problem

lecture36 The Dirichlet 0:24:41

lecture36 The Dirichlet Problem and Poisson's Theorem

PDE. Lecture #31. 0:30:52

PDE. Lecture #31. Weak Solution to the Dirichlet Problem for Poisson’s Equation

PDE Lecture 18 1:29:03

PDE Lecture 18 Dirichlet's problem in a ball

Lecture 22: Dirichlet 0:59:22

Lecture 22: Dirichlet boundary value problem for Laplace's equation on a disc

Section 2.1 - 0:05:52

Section 2.1 - Boundary Conditions

Solution method for 0:18:22

Solution method for the Diffusion Equation with Dirichlet BCs

MM58: Dirichlet and 0:10:48

MM58: Dirichlet and Von Neumann BC

undergraduate machine learning 0:46:40

undergraduate machine learning 23: Dirichlet and categorical distributions

mod04lec47 - Dirichlet 0:13:22

mod04lec47 - Dirichlet Conditions

Lecture 23: Physically 1:11:12

Lecture 23: Physically Based Animation and PDEs (CMU 15-462/662)

Math 462 - 1:22:26

Math 462 - Lecture 23

Lecture 23 0:07:45

Lecture 23 Problem on Euler Maclaurin Formula

Partial Differential Equation 0:39:45

Partial Differential Equation with Dirichlet Boundary Conditions (With Example)

Solution method for 0:13:46

Solution method for the Diffusion Equation with homogeneous Neumann and inhomogeneous Dirichlet BCs

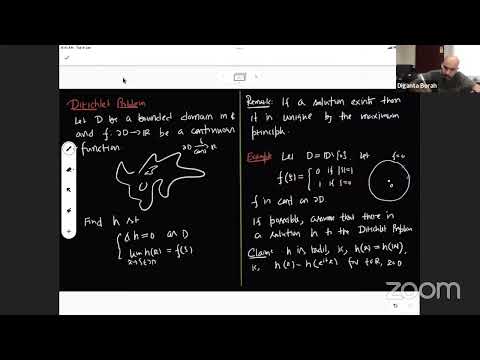
The Riemann Mapping 1:33:13

The Riemann Mapping Theorem via the Dirichlet problem | Prof. Diganta Borah | Day 2

Комментарии
Автор

Big thanks to MIT OCW. I’ve been able to refresh, familiarize, and learn: calculus, linear algebra, classical mechanics, electrodynamics, classical waves, quantum mechanics, and I’m now familiar with functional analysis. A fantastic resource!

GuitarSorcery
Автор

I have watched all videos of functional analysis. I did not know that
1. the notion of equi-small tails
2. the set of compact operaters is the closure of finite rank operators
3. the reason of name "resolvent"
4 Good example of compact operator
5, , ,, and many things I have learned through his 23 lectures.

I greatly appreciate his lecture. His lecture let me be close to functional analysis. Great lecture!
One thing I wanna order is that sometimes his voice is too small to hear, but anyway Great!

hausdorffm
Автор

He builds to the adjoint for trivial means. Well done.

SSNewberry
Автор

I think there is a little typo in the beginning of the proof of Theorem 241. It is stated: "... since m_V and A^(1/2) are compact operators, so ...". It should read: "... since A^(1/2)m_V and A^(1/2) are compact operators, so ...". Kind regards

enricods
Автор

Isn't at 16:06 RHS is C | \int f(y) | rather than C \int | f(y) |?

broccoloodle
Автор

Good lecture, but I have a comment:
1) At 25', the I checked the solution, it should by Does anyone check it?

abdelfetehfareh