filmov
tv
My favorite proof of the n choose k formula!
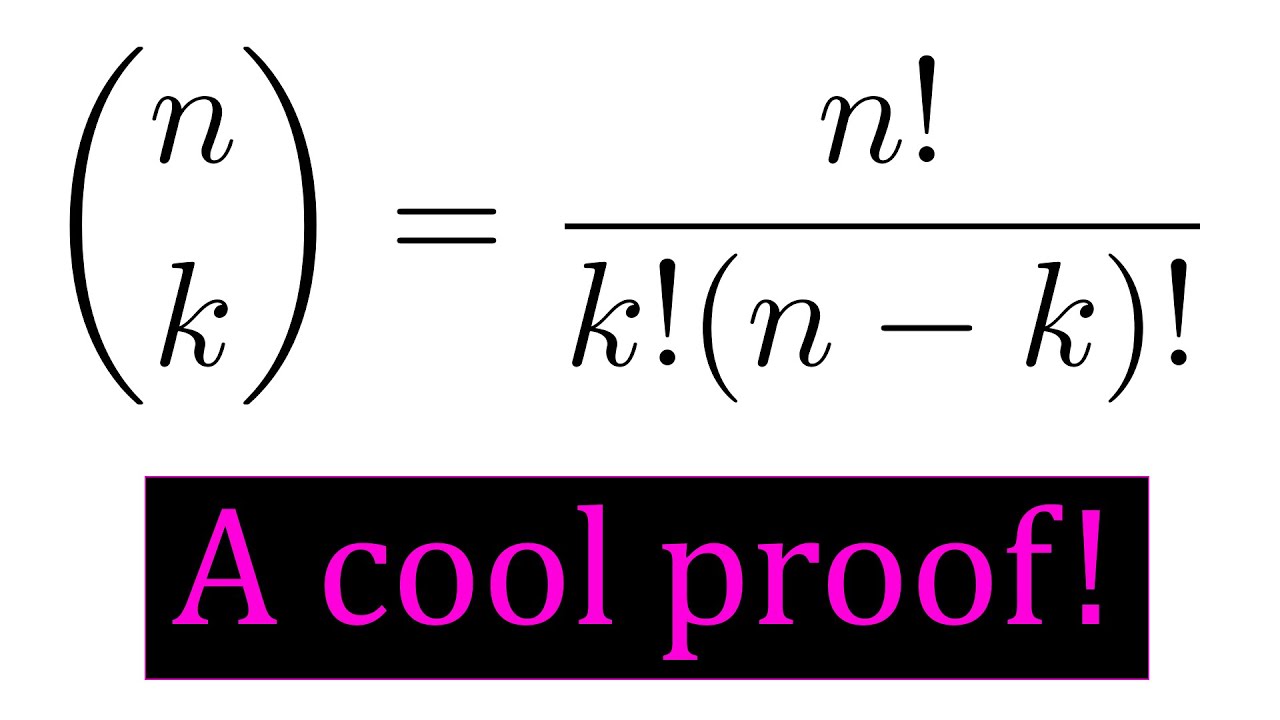
Показать описание
The binomial coefficient shows up in a lot of places, so the formula for n choose k is very important. In this video we give a cool combinatorial explanation of that formula!
Subscribe to see more new math videos!
Music: OcularNebula - The Lopez
Subscribe to see more new math videos!
Music: OcularNebula - The Lopez
My favorite proof of the n choose k formula!
The Pythagorean Theorem FAVORITE PROOF
Pythagorean Theorem & Its Inverse (my favorite proof)
my new favorite proof of this classic result
proof you’re not ugly😳 #confidence #shorts
a great proof of my favorite identity!!!
My new favorite proof of Fermat's little theorem!!
This Will Be Your Favorite Simple Problem
Astonishing Proof of Krishna's Existence! - Nilesh Oak #shorts
the famous Calculus proof of the Pythagorean theorem.
Proof Jesus is real😵 #shorts
A Mathematician’s View of Proof - Sarah Hart
Proof Andrea Had No Childhood
overpowered irrationality! #math #proof #squareroot
Visual proof every student should see
This Is My New Favorite Number
PROOF IM A COMPUTER
I USE TO LOVE THEM ...
my favorite infinite prime proof
Proof that God has favorites 😭 @Infamous_wu13 #sofimanassyan #relatable #funny
Fire proof suit #shorts
I found proof that the karate kid remake is young cobra Kai 🤣🤣🤣 #cobrakai
PROOF Sockie is the favorite child #norrisnuts
ASTONISHING EVIDENCE OF REINCARNATION | The Proof Is Out There | #Shorts
Комментарии
 0:13:36
0:13:36
 0:01:41
0:01:41
 0:08:12
0:08:12
 0:11:23
0:11:23
 0:00:12
0:00:12
 0:19:27
0:19:27
 0:15:44
0:15:44
 0:03:03
0:03:03
 0:00:52
0:00:52
 0:14:35
0:14:35
 0:00:23
0:00:23
 0:51:27
0:51:27
 0:00:24
0:00:24
 0:00:44
0:00:44
 0:00:57
0:00:57
 0:03:28
0:03:28
 0:00:50
0:00:50
 0:22:09
0:22:09
 0:00:52
0:00:52
 0:00:08
0:00:08
 0:00:27
0:00:27
 0:00:24
0:00:24
 0:00:57
0:00:57
 0:00:59
0:00:59