filmov
tv
A Non-Standard Trig Equation | sin(x)=2

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #ComplexNumbers #TrigonometryProblems
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
#exponentials #exponentialequations #exponential #exponents #challengingmathproblems #maths #math
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #ComplexNumbers #TrigonometryProblems
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
#exponentials #exponentialequations #exponential #exponents #challengingmathproblems #maths #math
A Non-Standard Trig Equation | sin(x)=2
Solve Trig Equations with non-standard period
solve non standard trig equations
Solving trig equations with non-standard periods using graph symmetry
A Non-Standard Trig Equation | cos(x)=2
GCSE Maths - All the Trigonometry Equations you Need To know! #119
Trig Identities
Trigonometry Concepts - Don't Memorize! Visualize!
Math 1175-05 - 29 August 2024 - Section 7.3
Sine of non special angle | Trig identities and examples | Trigonometry | Khan Academy
Finding Exact Trigonometric Value of Non-Standard Angles using Addition/Subtraction Trig Identities
Determining the equation of a trig function | Graphs of trig functions | Trigonometry | Khan Academy
Trigonometry: Solving for All Possible Solutions of a Trig Equation
Trick for doing trigonometry mentally!
How To Use Reference Angles to Evaluate Trigonometric Functions
Trigonometry: Solving Trig Equations
Solving an inverse trigonometric equation
Redefining the Trig Functions on the Unit Circle (1 of 2: The Basic Concept)
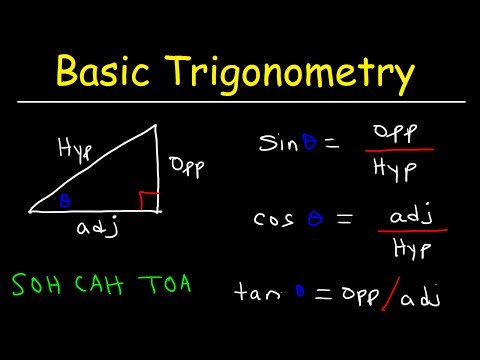
Trigonometry For Beginners!
Trig Substitution Two Non-Standard Examples
Precalculus - Solving Trig Equations with Non-Special Angles
Solving Trigonometric Equations: Adjusted Period Examples
How To Find The Exact Values of Trig Functions
Grade 11 Trig Topic 5.4 - Trig Equations Level 4
Комментарии
 0:10:02
0:10:02
 0:14:13
0:14:13
 0:08:25
0:08:25
 0:10:55
0:10:55
 0:09:19
0:09:19
 0:02:53
0:02:53
 0:27:57
0:27:57
 0:32:35
0:32:35
 1:06:20
1:06:20
 0:08:35
0:08:35
 0:13:18
0:13:18
 0:05:22
0:05:22
 0:05:17
0:05:17
 0:05:02
0:05:02
 0:10:59
0:10:59
 0:02:23
0:02:23
 0:07:37
0:07:37
 0:10:53
0:10:53
 0:21:52
0:21:52
 0:09:32
0:09:32
 0:20:25
0:20:25
 0:13:52
0:13:52
 0:12:39
0:12:39
 0:29:51
0:29:51