filmov
tv
Understanding Compact Sets
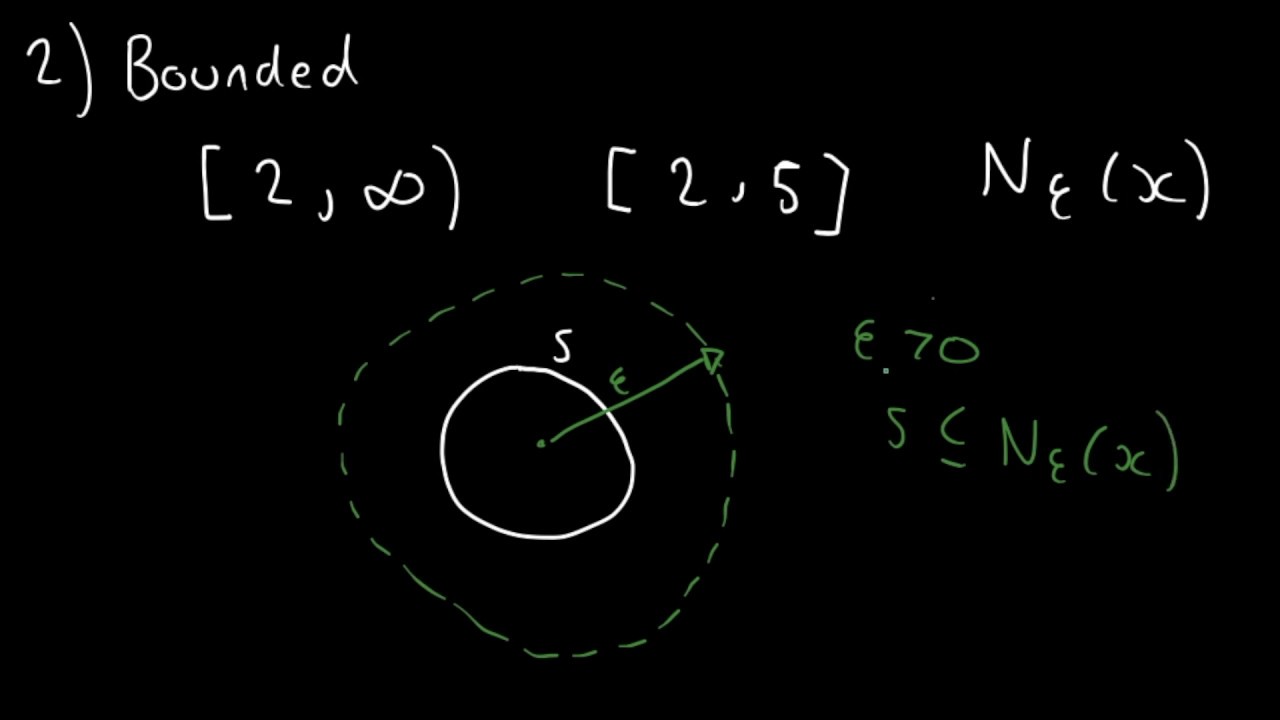
Показать описание
In this video I explain the definition of a Compact Set. A subset of a Euclidean space is Compact if it is closed and bounded, in this video I explain both with a link to a specific video about closed sets below.
Video explaining Epsilon Neighbourhood and Closed Set:
Video explaining Epsilon Neighbourhood and Closed Set:
Understanding Compact Sets
Open Covers, Finite Subcovers, and Compact Sets | Real Analysis
The Concept So Much of Modern Math is Built On | Compactness
Real Analysis 13 | Open, Closed and Compact Sets
Functional Analysis 16 | Compact Sets
Compactness
An Introduction to Compact Sets
Identifying Open, Closed, and Compact Sets | Real Analysis Exercises
Real Analysis | Compact sets, supremums, and infimums.
Chapter 0: [Real Analysis] Review 4: Closed and Compact sets
Manifolds 8 | Compactness
Lecture 3: Compact Sets in Rⁿ
Show that (0, 1] is not compact - Topology - Compact sets
Compactness
Topology Lecture 21: Compactness I
Properties of Compactness
Every Compact Set in n space is Bounded
Real Analysis | Compact set of real numbers.
Basic Concepts of Compact set
The Direct Image of a Compact Set Under a Continuous Function is Compact Proof
Sequential Compactness
Real Analysis 13 | Open, Closed and Compact Sets [dark version]
Non Compact set
Real Analysis 30 | Continuous Images of Compact Sets are Compact
Комментарии
 0:08:08
0:08:08
 0:13:58
0:13:58
 0:20:47
0:20:47
 0:09:28
0:09:28
 0:10:56
0:10:56
 0:22:38
0:22:38
 0:11:13
0:11:13
 0:07:54
0:07:54
 0:06:09
0:06:09
 0:14:36
0:14:36
 0:11:05
0:11:05
 1:16:43
1:16:43
 0:02:23
0:02:23
 0:37:56
0:37:56
 0:49:45
0:49:45
 0:19:32
0:19:32
 0:08:28
0:08:28
 0:08:38
0:08:38
 0:01:06
0:01:06
 0:06:42
0:06:42
 0:13:10
0:13:10
 0:09:15
0:09:15
 0:25:00
0:25:00
 0:07:04
0:07:04