filmov
tv
the octonions!
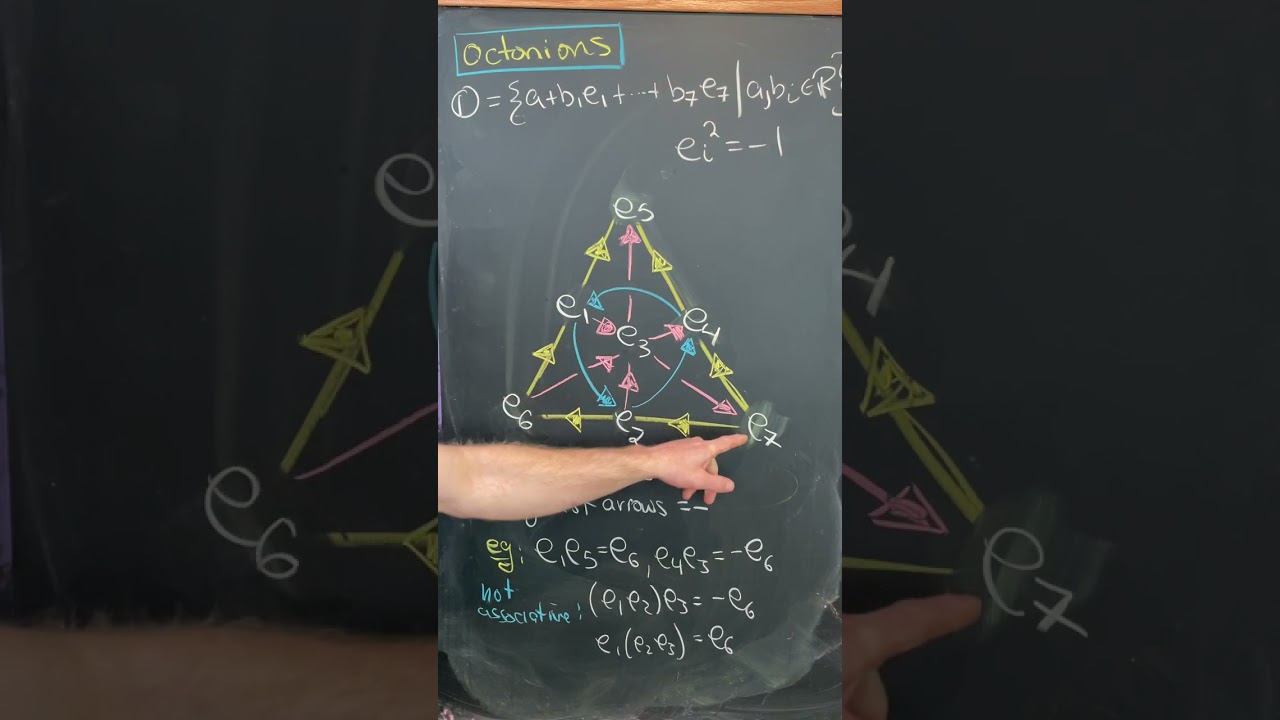
Показать описание
🌟Support the channel🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
Cohl Furey on the Octonions and Particle Physics
the octonions!
alternative algebra -- featuring the octonions!
Octonion
What Are Octonions?
Fitness levels of complex LSRDRs of the octonions during training
I trained an AI to rediscover the octonions
Rotations with Octonions
Spectra of real and complex LSRDRs of the octonions during training
Could These Numbers Unravel New Dimensions in Space?
Fantastic Quaternions - Numberphile
Alternative to String Theory (Octonions)
What are...octonions?
Fitness levels of real LSRDRs of the octonions during training
Discovery of Octonions #octonions #williamhamilton #quaternions #science
From Hamilton’s Quaternions to Graves & Cayley’s Octonions – Louis Kauffman
Introduction to the complex octonions (Video 8/14)
This Week's Finds 8: E8 and the octonions
Aikyons, Octonions, and Unification
Climbing past the complex numbers.
This Week's Finds 9: quaternions and octonions
Visualizing quaternions (4d numbers) with stereographic projection
What does octonion mean?
How to get around the non-associativity of the octonions (Video 9/14).
Комментарии
 0:01:51
0:01:51
 0:00:58
0:00:58
 0:19:55
0:19:55
 0:15:04
0:15:04
 0:00:59
0:00:59
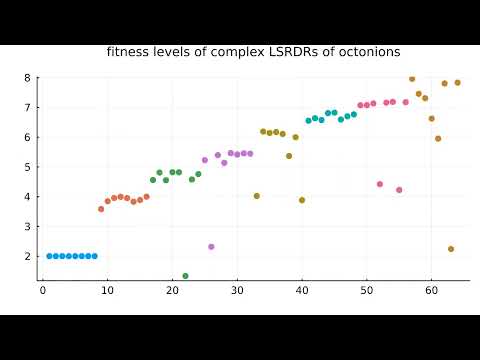 0:01:15
0:01:15
 0:01:03
0:01:03
 0:22:37
0:22:37
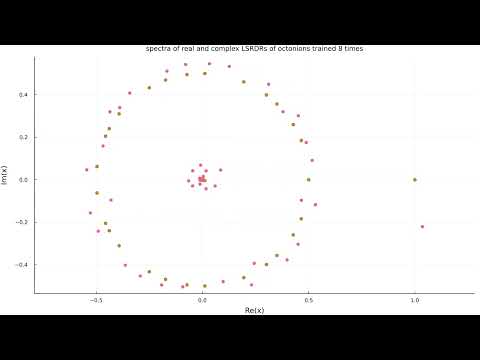 0:01:20
0:01:20
 0:06:05
0:06:05
 0:12:25
0:12:25
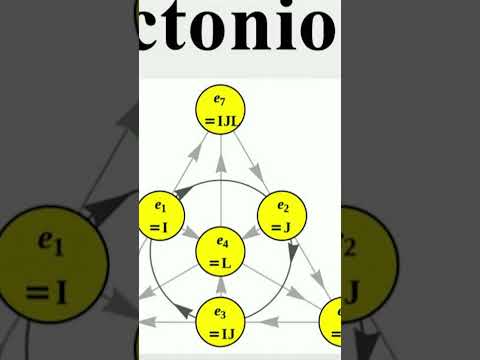 0:00:58
0:00:58
 0:13:52
0:13:52
 0:01:04
0:01:04
 0:00:15
0:00:15
 0:11:11
0:11:11
 0:05:19
0:05:19
 1:00:34
1:00:34
 0:14:46
0:14:46
 0:30:31
0:30:31
 0:55:47
0:55:47
 0:31:51
0:31:51
 0:00:34
0:00:34
 0:07:52
0:07:52