Fitness levels of real LSRDRs of the octonion-like algebra during training

The octonions are up-to-isomorphism, a unique 8 dimensional real inner product space O together with a bilinear operation * and a unit 1 such that ||x*y||=||x||*||y|| and 1*x=x*1=x for all x,y in O. The bilinear operation * is non-associative. While linear algebra extends to quaternionic matrices quite well (except for some quantum information theory), due to the non-associativity of the octonions, there is no reasonable theory of octonionic matrices. The octonions are therefore not as popular as the quaternions for this and other reasons.

We define an octonion-like algebra to be an 8 dimensional real inner product space A together with a bilinear operation * such that ||x*y||=||x||*||y|| for all x,y in A. Let A be an octonion-like algebra.

Let e_1,...,e_8 be an orthonormal basis of A. Let A_1,...,A_8 be the linear operators from A to A defined by setting A_j x=e_j *x. Then the operators A_1,...,A_8 are orthogonal.

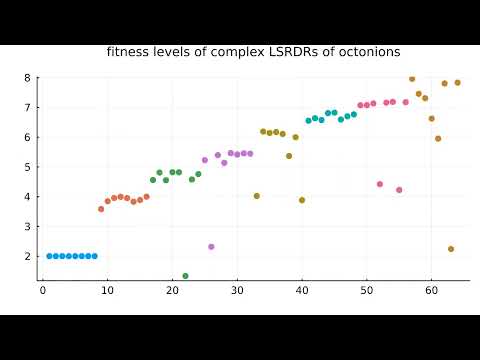
Let d be a natural number at most 8. Let B_1,...,B_8 be d by d real matrices. Then we say that the fitness level of B_1,...,B_8 is
rho(kron(A_1,B_1)+...+kron(A_8,B_8))^2
rho(kron(B_1,B_1)+...+kron(B_8,B_8)).

'rho' stands for the spectral radius. 'kron' stands for the Kronecker product. While I have stated the fitness function in terms of bases and coordinates, we can reformulate everything in this animation without referring to any specific bases.

For each d from 1 to 8, we maximize the fitness level of the d by d real matrices B_1,...,B_8 eight different times using gradient ascent, and we show all 64 fitness levels of the local maximization during the course of the gradient ascent. Each value d in {1,...,8} is assigned a different color in the visualization, and lower values of d are put to the left of the higher values of d.

Since we are using power iteration to calculate the spectral radius and gradient, near the beginning of the visualization, the calculated fitness levels are unstable. We observe that for each particular value d, and each instance of the gradient ascent, we attain a fitness level of precisely d. We also have a (not yet proven) description of all global maxima for this fitness function.

Suppose that d is in {1,...,8}. Suppose that R is a d by 8 real matrix and S is an 8 by d real matrix and SR is an orthogonal projection operator. Then if we set B_j=RA_j S for all j, then (B_1,...,B_8) is presumably a local maximum for our fitness function and all global maxima for our fitness function are of this form. The dominant eigenvalue of kron(A_1,B_1)+...+kron(A_8,B_8) also has a simple description. Let G be the superoperator mapping 8 by 8 matrices to the 8 by 8 matrices defined by setting G(X)=A_1 X transpose(A_1)+...+PA_8P X transpose(PA_8P). Then G is similar to a direct sum of kron(A_1,B_1)+...+kron(A_8,B_8) and a zero matrix, but the dominant eigenvector of G is the matrix P.

The notion of an LSRDR is my own. I have made this visualization in order to demonstrate some of the interesting properties of both the octonion-like algebras and LSRDRs. I cannot see any way that the fitness levels of these LSRDRs could have a simpler interpretation (but producing a mathematical proof that 1,2,3,4,5,6,7,8 are the global maximum values may take some work). This simplicity of the fitness levels demonstrates that the octonion-like algebras are elegant mathematical structures and that LSRDRs behave mathematically in a way that is compatible with the octonion-like algebras. We should strive for this level of interpretability in machine learning, and we should develop machine learning algorithms that behave as mathematically as LSRDRs.

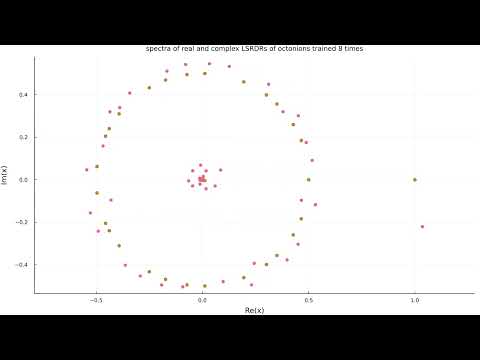
We observe that the fitness levels of the real LSRDRs are strictly lower than the fitness levels of the corresponding complex LSRDRs of A_1,...,A_8 when the dimension is kept the same. This demonstrates that while the real and complex LSRDRs of matrices often coincide, there are instances where the real LSRDR has a lower fitness than the corresponding complex LSRDR.

Correction: While the visualization title says ". . . LSRDRs of octonions", it is more accurate to say ". . . LSRDRs of octonion-like algebras"