filmov
tv
Integration by Parts
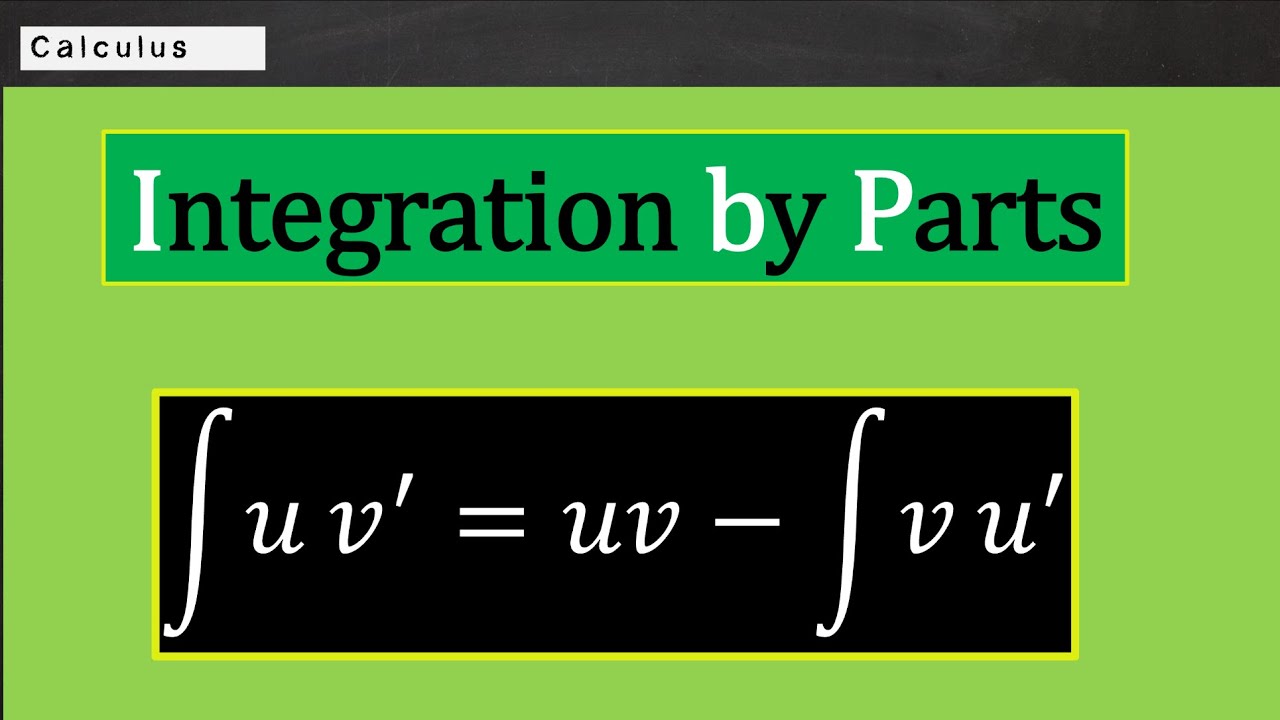
Показать описание
In this video, I showed how and when to use the Integration by Parts technique for integration.
Watch the other video here:
Watch the other video here:
Integration By Parts
What is Integration by Parts - How to do Integration by Parts
Integration By Parts
integration by parts, DI method, VERY EASY
Integration by Parts... How? (NancyPi)
Integration by parts (visualised)
Calculus 2 Lecture 7.1: Integration By Parts
Integration by parts intro | AP Calculus BC | Khan Academy
Integration By Parts - Tabular Method
Two Tricky Integration By Parts Examples
Integration by Parts
life changing integration by parts trick
Integration By Parts | Calculus 2 Lesson 11 - JK Math
Why I don't teach LIATE (integration by parts trick)
Integration by Parts
Integration by Parts
Integration by parts
I Integrate By Parts (Total Eclipse of the Heart Parody)
Calculus 2: Integration by Parts (Video #1) | Math with Professor V
Integration by Parts (introduction & 2 examples)
Integration by Parts | Calculus
Integration by Parts EXPLAINED in 5 Minutes with Examples
Integration By Parts Formula Derivation
Integration by Parts (1 of 3: Deriving the Formula)
Комментарии
 0:32:52
0:32:52
 0:03:57
0:03:57
 0:13:17
0:13:17
 0:16:59
0:16:59
 0:18:00
0:18:00
 0:08:54
0:08:54
 1:54:37
1:54:37
 0:03:52
0:03:52
 0:18:10
0:18:10
 0:08:35
0:08:35
 0:25:12
0:25:12
 0:05:23
0:05:23
 0:41:46
0:41:46
 0:14:54
0:14:54
 0:15:21
0:15:21
 0:26:33
0:26:33
 0:17:00
0:17:00
 0:04:38
0:04:38
 0:29:38
0:29:38
 0:13:18
0:13:18
 0:11:04
0:11:04
 0:05:46
0:05:46
 0:05:13
0:05:13
 0:05:05
0:05:05