Multivariable Calculus | ArcLength

preview_player
Показать описание
We derive the formula for the arclength of a curve.

  1. Michael Penn
  2. math
  3. mathematics
  4. calculus
  5. Randolph College
  6. randolph
Рекомендации по теме
Multivariable Calculus | 0:04:10

Multivariable Calculus | ArcLength Example

The Arc Length 0:07:43

The Arc Length of a Vector Function

Curves, Parameterizations, and 0:10:04

Curves, Parameterizations, and the Arclength Parameterization

Multivariable Calculus | 0:12:18

Multivariable Calculus | ArcLength

How long is 0:07:10

How long is a curve?? The Arclength Formula in 3D

Calculus 3 Lecture 2:12:45

Calculus 3 Lecture 12.3: Arc Length/Parameterization, TNB (Frenet-Serret) Intro

arc length of 0:09:39

arc length of a vector function (KristaKingMath)

Arc Length of 0:12:34

Arc Length of Parametric Curves

Multivariable Calculus: Arc 0:09:06

Multivariable Calculus: Arc length and the arc length function

Arc Length (Calculus 0:09:39

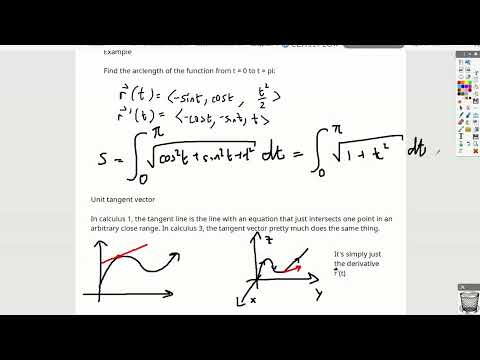
Arc Length (Calculus 3)

Arc Length (formula 0:07:57

Arc Length (formula explained)

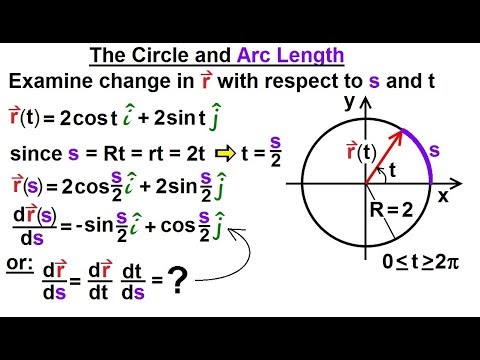
Calculus 3: Vector 0:03:22

Calculus 3: Vector Calculus in 2D (28 of 39) The Circle and Finding Arc Length

Multivariable Calculus Unit 0:35:36

Multivariable Calculus Unit 8: Arc length and Curvature

Multivariable Calculus 9 0:22:50

Multivariable Calculus 9 - Arc Length and the TNB-Frame

Multivariable Calculus | 0:17:47

Multivariable Calculus | Definition of line integral with respect to arclength.

7: Arc Length 0:04:59

7: Arc Length of Curves - Valuable Vector Calculus

How to compute 0:10:33

How to compute a tangent vector and arc length of a curve

Arc Length of 0:14:54

Arc Length of Curve | Numericals | Parametrization of Curve | Application | Vector Calculus | Maths

Multivariable Calculus - 0:20:46

Multivariable Calculus - Arc Length and Area with Parametric Equations

Calculus 3: How 0:11:22

Calculus 3: How to reparametrize a vector function (with respect to arc length)

Arc length of 0:07:06

Arc length of a vector function - Vector Calculus

reparametrizing the curve 0:07:57

reparametrizing the curve in terms of arc length (KristaKingMath)

Multivariable Calculus | 0:29:28

Multivariable Calculus | 2.3 Arclength and Curvature

Calculus(III) : Arc 0:03:36

Calculus(III) : Arc Length in Space : Vector Calculus

Комментарии
Автор

I'm really amazed by all your content. Whenever I doubt about something I search your channel

MrCentrax
Автор

This video make so much meaning and I can understand a lot from it very well done thank you.

georgettebeulah
Автор

If you cut the cylinder vertically, you get a square with side 2pi and the helix is the diagonal.

byronwatkins
Автор

Always nice. I comment to improve your visibility.

ChaineYTXF
Автор

how formal would you say this playlist(Multivariable Calculus) is ? How rigorous are the proofs compared to textbook such as e.g. Shifrin's Multivariable Mathematics

-sn
Автор

Your video does a great job of explaining the intuition behind the formula for arclength. The only part I'm confused about is the use of the MVT (6 minute mark). The single variable calulus MVT gives us a t* for each component of the vector valued function r, but would not seem to imply that we have a single t* that works for every component of r. That is, we might have n different t*, one for r1, another for r2, etc. Can you help with this? Thanks for all the work you put into these great videos.

dewookus