Lecture 5: Runtime Complexity of algorithms

The Design and Analysis of Algorithms course covers a comprehensive range of topics to build a solid understanding of algorithmic principles and techniques.
The course begins with the pre-requisite topics of Data Structures. After this, an introduction to algorithms, emphasizing their importance and efficiency,
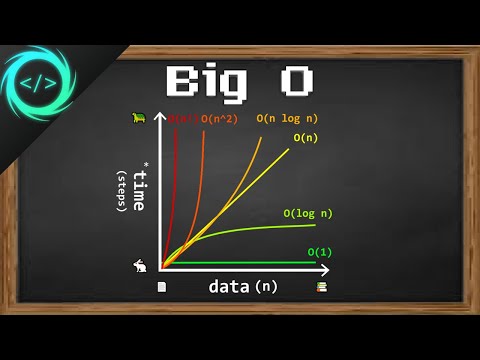
along with the analysis of time and space complexity
using Big-O, Big-Theta, and Big-Omega notations. It then delves into the divide-and-conquer technique, exploring algorithms like Merge Sort, Quick Sort,
and Binary Search, and analyzing recurrence relations using methods such as substitution and the Master Theorem. Greedy algorithms are also a key focus,
with applications in problems like Minimum Spanning Tree (using Kruskal’s and Prim’s algorithms), Huffman encoding, and Activity Selection, emphasizing
scenarios where greedy approaches yield optimal solutions. The course further examines dynamic programming, solving problems like the Longest Common
Subsequence, Knapsack, and Matrix Chain Multiplication, highlighting the concepts of overlapping subproblems and optimal substructure. Additionally,
graph algorithms such as Depth-First Search (DFS), Breadth-First Search (BFS), shortest path algorithms (Dijkstra’s and Bellman-Ford), and network flow
problems are explored in depth. The semester concludes with an introduction to NP-completeness, covering the classification of problems into P, NP, and
NP-complete categories, along with examples like the Traveling Salesman Problem (TSP) and satisfiability (SAT), providing insights into advanced
computational complexity and intractable problems.