Approximation properties of Taylor polynomials Suppose that f(x) is differentiable on an interval c…

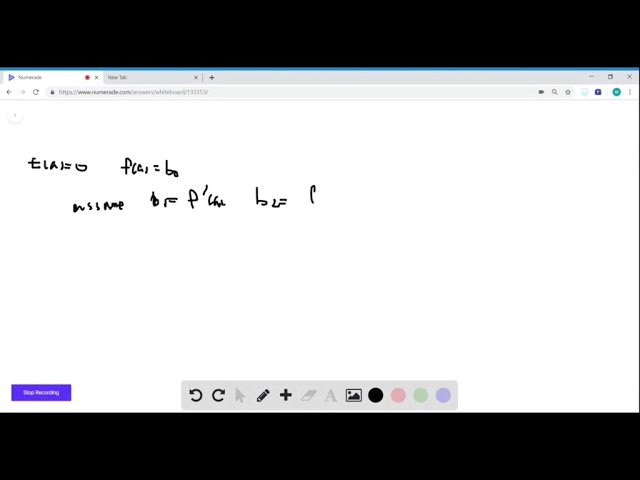
Approximation properties of Taylor polynomials Suppose that f(x) is differentiable on an interval centered at x=a and that g(x)=b_0+b_1(x-a)+⋯+b_n(x-a)^n is a polynomial of degree n with constant coefficients b_0, …, b_n . Let E(x)= f(x)-g(x) . Show that if we impose on g the conditions i) E(a)=0 ii) lim_x →a E(x)/(x-a)^n=0 then [ g(x)=f(a)+f^'(a)(x-a)+f^''(a)/2 !(x-a)^2+⋯; +f^(n)(a)/n !(x-a)^n ]. Thus, the Taylor polynomial P_n(x) is the only polynomial of degree less than or equal to n whose error is both zero at x=a and negligible when compared with (x-a)^n.

Watch the full video at:

Never get lost on homework again. Numerade is a STEM learning website and app with the world’s largest STEM video library.
Join today and access millions of expert-created videos, each one skillfully crafted to teach you how to solve tough problems step-by-step.

Join Numerade today at:

exploring the versatile applications of taylor polynomials
#DiscovertheBestSeriestoBinge-Watch|YourUltimateGuide #ExploringtheVersatileApplicationsofTaylorPolynomials