filmov
tv
Sketching Rational Functions Having Removable Discontinuities

Показать описание
Follow us:
A removable discontinuity is a point on the graph that is undefined or does not fit the rest of the graph. If you find a restriction in the function that can be canceled out, this will result in a hole leading to a removable discontinuity.
Q1. Sketch the graph of f(x)=(x^2−1)/(x+1), and find the coordinates of all removable discontinuities.
Q2. Sketch the graph of f(x)=(x+3)/(x^2+x−6), and find the coordinates of all removable discontinuities.
 0:04:36
0:04:36
 0:01:02
0:01:02
 0:04:49
0:04:49
 0:07:19
0:07:19
 0:05:59
0:05:59
 0:34:52
0:34:52
 0:00:44
0:00:44
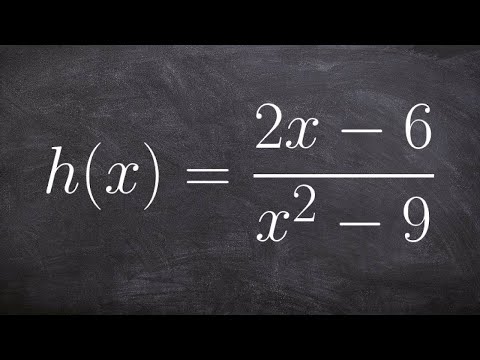 0:02:16
0:02:16
 0:07:22
0:07:22
 0:22:27
0:22:27
 0:04:43
0:04:43
 0:04:51
0:04:51
 0:04:34
0:04:34
 0:43:04
0:43:04
 0:07:41
0:07:41
 0:38:45
0:38:45
 0:07:18
0:07:18
 0:02:14
0:02:14
 0:10:58
0:10:58
 0:25:33
0:25:33
 0:03:54
0:03:54
 0:03:07
0:03:07
 0:11:42
0:11:42
 0:06:20
0:06:20