filmov
tv
La Trasformata Z: Definizione proprietà esempi numerici. Segnali discreti

Показать описание
In questo video parleremo della trasformata z. Vedremo come passare da un segnale discreto ad una funzione complessa. Segnali a tempo discreto. Proprietà ed esempi di calcolo.
#trasformata #matematica #segnali #yousciences
Altri "video meccatronici" ⚛️:
Dove trovarmi 💎:
➤INSTAGRAM: @yousciences @___giux___
📽️ VIDEO STREAM ALL:
Chapter summary
00:00 Introduzione
01:00 Segnali a tempo discreto
03:15 La Trasformata Z
07:30 Raggio di Convergenza, ROC
08:07 Antitrasformata
12:45 Proprietà della Z-Trasformata
13:10 Esempio I: serie unitaria
15:40 Esempio II: Delta di Dirac
17:12 Esempio III: Esponenziale complesso
18:50 A cosa servono le trasformate?
Graphics / Editing / Audio / Direction - by GIUX
#trasformata #matematica #segnali #yousciences
Altri "video meccatronici" ⚛️:
Dove trovarmi 💎:
➤INSTAGRAM: @yousciences @___giux___
📽️ VIDEO STREAM ALL:
Chapter summary
00:00 Introduzione
01:00 Segnali a tempo discreto
03:15 La Trasformata Z
07:30 Raggio di Convergenza, ROC
08:07 Antitrasformata
12:45 Proprietà della Z-Trasformata
13:10 Esempio I: serie unitaria
15:40 Esempio II: Delta di Dirac
17:12 Esempio III: Esponenziale complesso
18:50 A cosa servono le trasformate?
Graphics / Editing / Audio / Direction - by GIUX
La Trasformata Z: Definizione proprietà esempi numerici. Segnali discreti
La trasformata Z in meno di un minuto! #matematica #ingegneria
mmi2021L08a definizione di Z trasformata
La TRASFORMATA DI LAPLACE: Definizione, Poli, Convergenza. Esempi
Che cos'è la Trasformata di Laplace: Definizione, esempi - Calcolo
mmi2021L08b proprietà Z trasformata
19 Trasformate 1/2
I Prodigi della TRASFORMATA di FOURIER
Trasformata di Fourier
mmi2021L14a definizione di trasformata di Laplace
Esercizi integrali difficili - Integrale sinx/x da 0 all'infinito con trasformata di Laplace
mmi2021L08c inversione della Z trasformata
20 Trasformate 2/2
mmi2021L10b discussione sulla Z trasformata di seno
Introduction to the Unilateral Z-Transform
mmi2021L15c alcuni esempi di trasformate
mmi2021L14b trasformata di segnali a supporto limitato e segnali periodici
Z transformation
Z-Transform Poles and Zeros
Intro to the Laplace Transform & Three Examples
Laplace Transformation|| Complete explanation with examples. #laplace #ode
FSD 2018 - Lezione 18 - Calcolo della funzione di transizione in s, Zeta trasformata
ADSP - 01 Quantization - 02 Quantization Definition
mmi2021L15e trasformata della derivata
Комментарии
 0:20:50
0:20:50
 0:00:58
0:00:58
 0:19:29
0:19:29
 0:15:47
0:15:47
 0:20:36
0:20:36
 0:34:44
0:34:44
 0:22:53
0:22:53
 0:19:37
0:19:37
 0:39:36
0:39:36
 0:32:48
0:32:48
 0:23:03
0:23:03
 0:19:35
0:19:35
 0:34:39
0:34:39
 0:15:37
0:15:37
 0:03:17
0:03:17
 0:15:54
0:15:54
 0:22:16
0:22:16
 0:00:14
0:00:14
 0:10:18
0:10:18
 0:12:05
0:12:05
 0:09:58
0:09:58
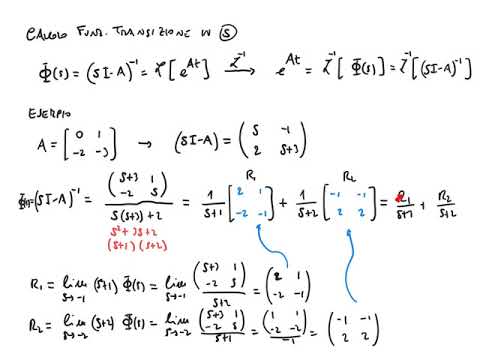 1:27:22
1:27:22
 0:03:31
0:03:31
 0:23:09
0:23:09