filmov
tv
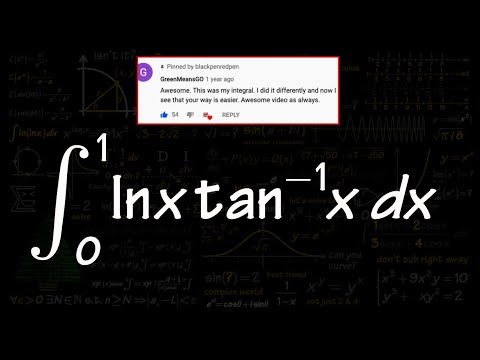
Integral of ln(x)*tan^-1(x) from 0 to 1

Показать описание
Integral of ln(x)*arctan(x) from 0 to 1,
Check out my site & social media
Check out my site & social media
integral from 0 to 1 of ln(x)tan^-1(x)
Integral of ln(x)*tan^-1(x) from 0 to 1
Integral of ln(x) fast!
How REAL Men Integrate Functions
integral of x*tan^ -1(x), calculus 2 tutorial, integration by parts
why integral of 1/x gives ln(x)+C #apcalculus
integral of ln(x) from 0 to 1
Integration by Parts tan ^(-1) 1/x dx over [0, sqrt(3)] example 18. LIATE. Evaluate
when calculus students use trig identities too early
Integral of lnx
Integral of tan^-1(x)
A cutie integral | integral ln tanx from 0 to pi/4
Integrate ln(x) from 0 to 1 (NO CALCULATION !)
integration of ln(tanx) from 0 to pi/2
Integral of ln(x) with 'infinite' integration by parts
IIT Bombay CSE 😍 #shorts #iit #iitbombay
Classic Integral ln(ln(x))/x #calculus #calculushelp #mathematics #integrationtricks #integrals
Integral of ln(x+1/x)/1+x^2 from 0 to inf
What is the integral of x ln x dx from 0 to 1?What is integral of 1 x?Why is 1 x integral lnx?
Integral x tan^-1 x easiest solution by Dig Your Mind
Integral ln(x)/(1+x) dx
integral of ln(x)/(x-1) from 0 to 1, integration with power series,
`int _(0) ^(1) x tan ^(-1) x dx =`
∫ln(x) dx = ? Solving integration of ln(x) using DI Table method.
Комментарии
 0:05:55
0:05:55
 0:17:49
0:17:49
 0:00:45
0:00:45
 0:00:35
0:00:35
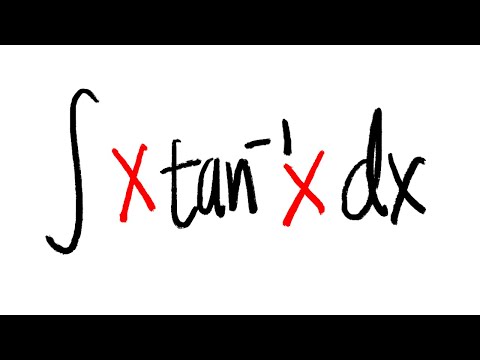 0:05:04
0:05:04
 0:00:34
0:00:34
 0:11:27
0:11:27
 0:05:57
0:05:57
 0:00:43
0:00:43
 0:01:26
0:01:26
 0:04:09
0:04:09
 0:08:08
0:08:08
 0:01:28
0:01:28
 0:07:44
0:07:44
 0:00:59
0:00:59
 0:00:11
0:00:11
 0:00:37
0:00:37
 0:05:47
0:05:47
 0:01:01
0:01:01
 0:04:08
0:04:08
 0:01:18
0:01:18
 0:17:29
0:17:29
 0:04:55
0:04:55
 0:00:50
0:00:50