Absolute Convergence, Conditional Convergence, and Growth Regressions

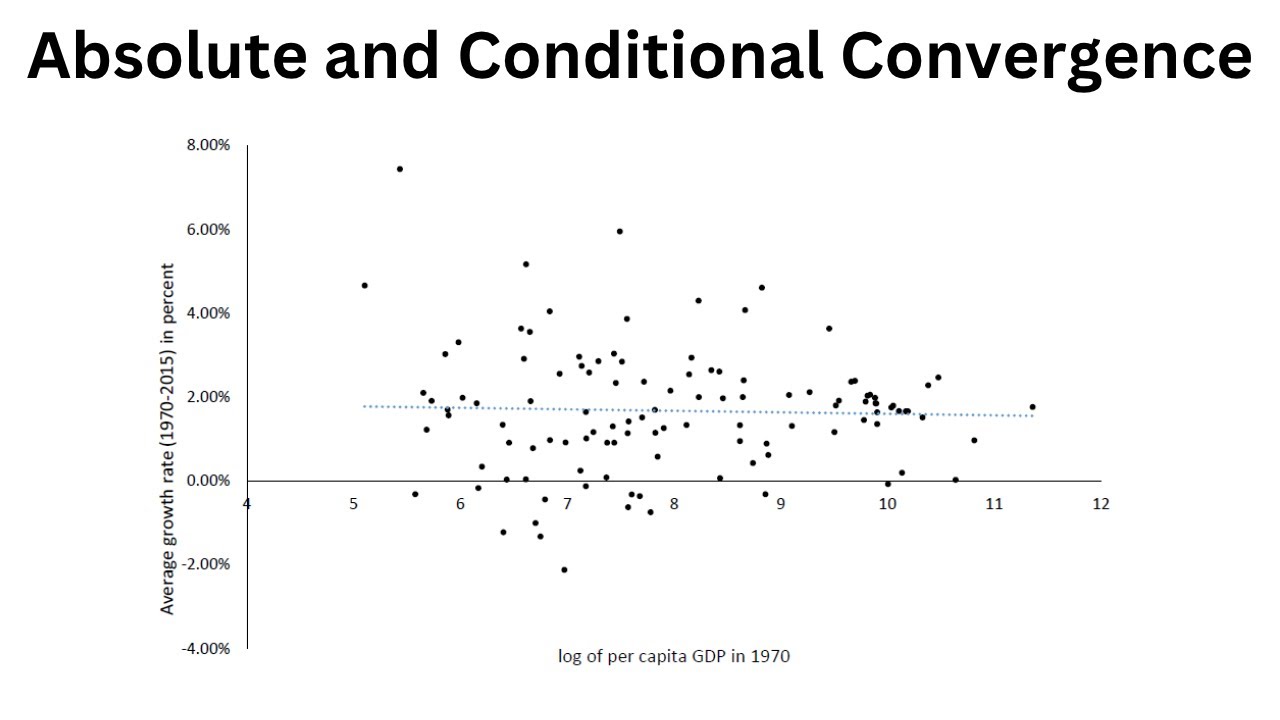
I use the Solow model to describe the process of convergence. In doing so, I show that the Solow model predicts "conditional convergence" (that countries sharing the same steady state will converge in terms of their per capita incomes) but not absolute convergence (that all countries irrespective of their steady state will converge). I then move on to explain the main idea behind growth regressions and how they are used to test for convergence. Finally, I dicuss problems in the context of growth regressions such as reverse causality, omitted variables, and p-hacking and highlight some potential solutions.

[PrinceAmankwah-yv]

Greetings and thank you for your insightful presentation. I learnt a lot. Please i have a question regarding initial capital variable. In a panel data of 48 countries spanning 1996-2021, what will be the variable "initial capital" if the definition is log of initial GDP per capita? How can I this variable for the my equation. Your help is greatly appreciated Sir

[sixsixsix]

Good evening, I would like to ask something about the econometric formulation of the equation of convergence.

In several articles such as Barro & Sala-I-Martin, 2004

When they calculate the average Growth rate for a period i.e 1970 - 2015 they use this method 1/T ( ln(gdp2015/gdp1970))

But in Mankiw et. al., 1992 I noticed that they simply take the logarithmic difference of GDP per capita for the period under consideration.
To match this with the example in the video:

ln(gdp2015/gdp1995)

Is this method correct? and if so what is the difference?