filmov
tv
cos(x)=x
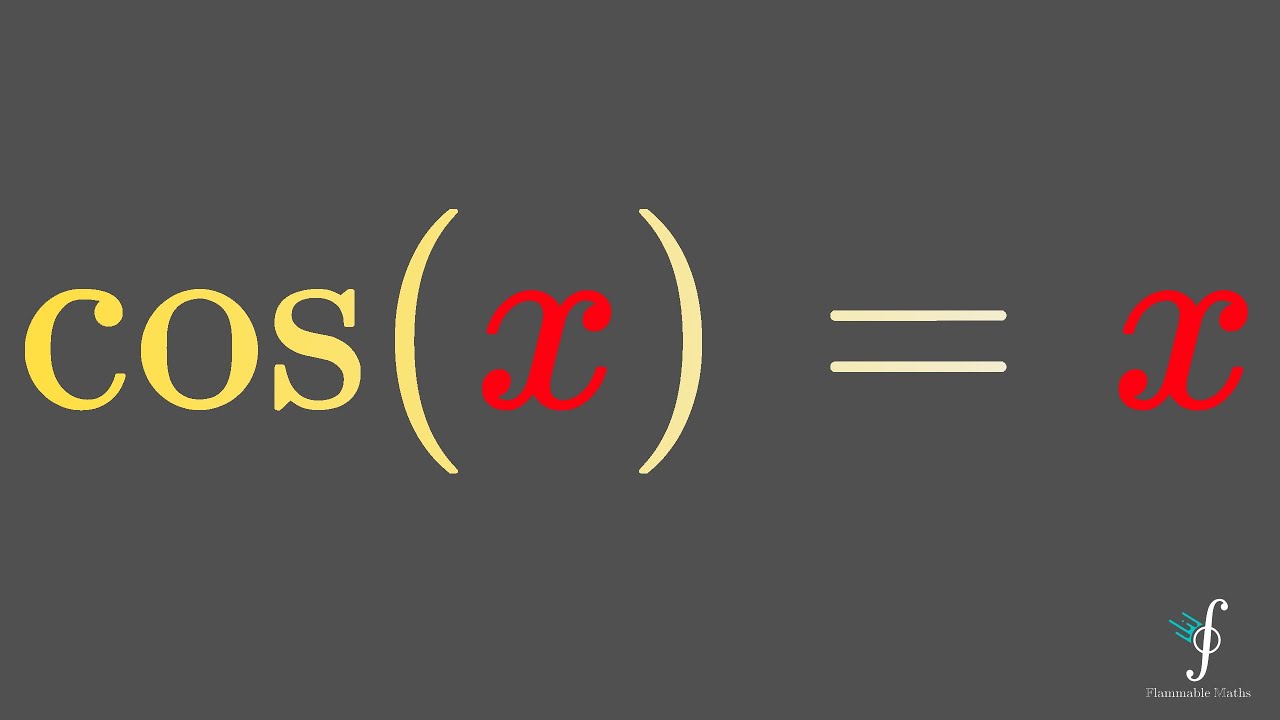
Показать описание
Today we calculate the transcendental number called "Dottie Number", which is the unique solution to the fixed point equation cos x=x . We use the Lagrange Inversion Theorem to get a perfectly disgusting series solution that is a numerical horror show. Enjoy! :D
Help me create more free content! =)
--------------------------------------------------------------------------------
Wanna send me some stuff? lel:
Postfach 11 15
06731 Bitterfeld-Wolfen
Saxony-Anhalt
Germany
--------------------------------------------------------------------------------
cos(x)=x
what’s the derivative of (cos(x))^x?
Théorème des valeurs intermédiaires et fonction trigonométrique - nombre de solution x=cos(x) 💡💡💡💡...
C𝗼𝘀 (-𝘅) = C𝗼𝘀 (𝘅) but WHY ❓
Integration of cosx/x (Solution)
Number of solutions of the equation cosx=x.
Why cos(-x)= cosx?
cos(3x) in terms of cos(x)
As funções trigonométricas cos(x) e sen(x) são muito estudadas
Nullstellen bei cos(x), trigonometrische Funktionen | Mathe by Daniel Jung
Derivative of sin(x) and cos(x), PROOF
72. Límite trigonométrico: 1 - cos x entre x, racionalizando | Límite
Verify the Trigonometric Identity cos(pi + x) = -cos(x)
Find the second order derivative of the function x.cos x Ncert continuity and Differentiation
Proof of the derivative of cos(x) | Derivative rules | AP Calculus AB | Khan Academy
cos(4x) in terms of cos(x)
LIMITE (1 - COSX)/X QUANDO X TENDE A ZERO /CÁLCULO 1/LIMITE DE UMA FUNÇÃO/LIMITE TRIGONOMÉTRICO
04 Limit of Cos X Minus 1 Over X
Limit of (1-cos(x))/x as x approaches 0 | Derivative rules | AP Calculus AB | Khan Academy
Taylor Series for f(x)+cos(x) Centered at x=0: Maclaurin Series
(sqrt(cos(x))*cos(200x)+sqrt(abs(x))-0.7)*(4-x*x)^0.01, sqrt(9-x^2), -sqrt(9-x^2) from -4.5 to 4.5
Maclaurin series of Cos(x)
Calculus Product Rule Example f(x) = sin(x)*cos(x)
Why does cos(t)=x and sin(t)=y?
Комментарии
 0:17:42
0:17:42
 0:02:43
0:02:43
 0:19:08
0:19:08
 0:06:20
0:06:20
 0:02:42
0:02:42
 0:02:16
0:02:16
 0:12:20
0:12:20
 0:04:46
0:04:46
 0:05:56
0:05:56
 0:02:52
0:02:52
 0:09:18
0:09:18
 0:05:16
0:05:16
 0:02:55
0:02:55
 0:02:39
0:02:39
 0:03:18
0:03:18
 0:05:33
0:05:33
 0:08:37
0:08:37
 0:05:33
0:05:33
 0:04:05
0:04:05
 0:02:31
0:02:31
 0:00:30
0:00:30
 0:04:57
0:04:57
 0:01:03
0:01:03
 0:03:56
0:03:56