filmov
tv
Complex Exponential Function || Lec 17 || Professor Maqsood Ali Abbas
Показать описание
#Exponentail_Function #Complex_Exponential_function #Coplex_function #maqsood #urdu #hindi #bs #ms #complexanalysis
Exponential form to find complex roots | Imaginary and complex numbers | Precalculus | Khan Academy
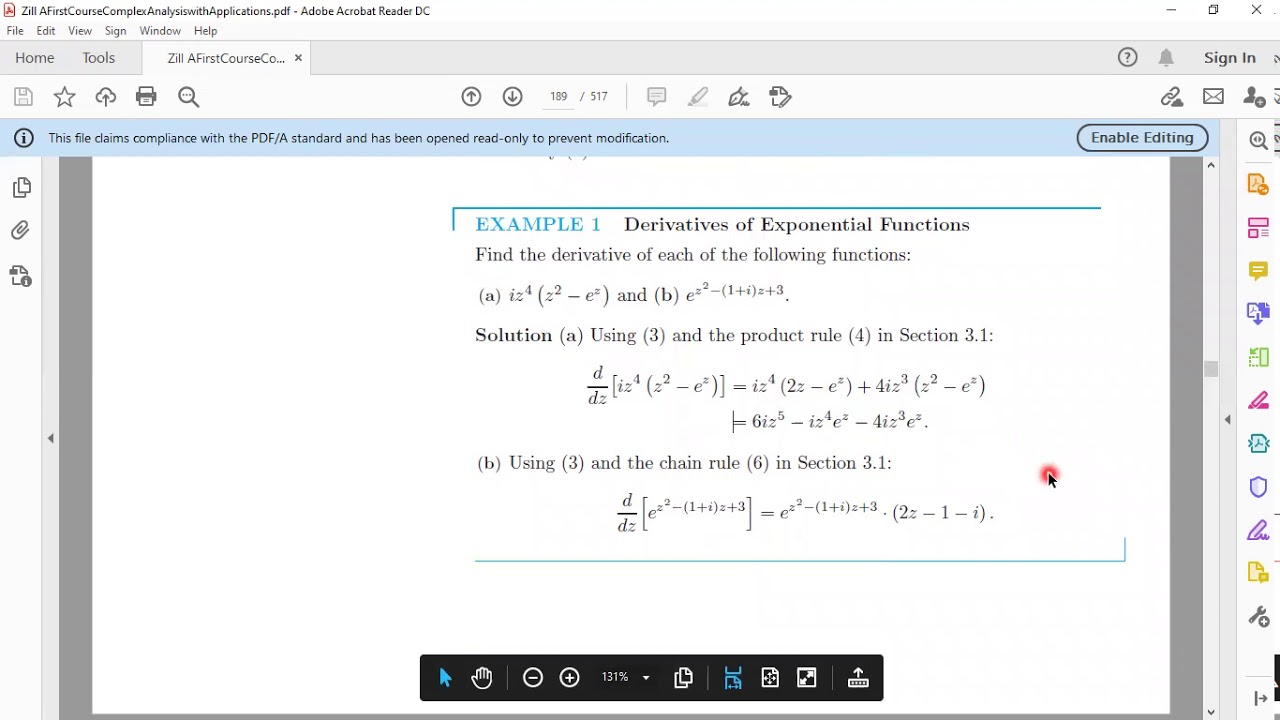
The complex exponential
Complex Exponential Function || Lec 17 || Professor Maqsood Ali Abbas
Intro Complex Analysis, Lec 16, Taylor Polynomials, Complex Exponential, Trig & Hyperbolic Funct...
Complex Analysis Episode 12: The Complex Exponential Function
Complex exponential function
w106 The complex exponential function
Lec#34||Elementary Functions||Complex Exponential function||Complex Analysis by Dennis G.Zill
LEC 78 | CHAP 06 | Ex 6.2 |INTEGRATION BY PARTS SPECIAL CASES | CLASS 12 MATH IFBISE & KPK NEW B...
Complex Analysis - Exponential Function
MAT132 Lec 32 2011 11 14 Complex Exponential; Intro to Diff Eqn's SUNY Stony Brook
Mappings by the exponential function
Complex analysis lec#12 (2/2) Examples of exponential function
Lec-46 | Complex Valued Exponential Function | Periodicity | Complex Analysis (Part-7)
The beauty of the complex exponential -- Complex Analysis 4
Intro Complex Analysis, Lec 6, Exponential Map on Mathematica, Squaring Map, Intro to Topology
Lec 45 - Exponential Functions: Definitions
complex analysis lec#12 (1/2)Complex Exponential Function in urdu/hindi
Signals: Complex Exponentials
Lec#11|Complex Function|Exponential Function| Polar coordinates|Complex analysis by Dennis G. Zill
lec 13 complex analysis Some results about exponential functions
Elementary Functions - 1) Exponential, Trigonometric, Logarithmic and Complex exponent functions
Lec 54 - Solving Exponential Equations
Mod-01 Lec-01 Analytic functions of a complex variable (Part I)
Комментарии
 0:11:53
0:11:53
 0:06:46
0:06:46
 0:17:15
0:17:15
 0:51:44
0:51:44
 0:04:30
0:04:30
 0:14:06
0:14:06
 0:05:54
0:05:54
 0:37:37
0:37:37
 0:33:48
0:33:48
 0:10:36
0:10:36
 0:54:00
0:54:00
 0:14:39
0:14:39
 0:11:08
0:11:08
 0:27:20
0:27:20
 0:29:48
0:29:48
 0:56:27
0:56:27
 0:13:42
0:13:42
 0:10:40
0:10:40
 0:03:37
0:03:37
 0:37:04
0:37:04
 0:27:35
0:27:35
 0:10:45
0:10:45
 0:17:56
0:17:56
 0:37:01
0:37:01