filmov
tv
Finding the value of x+y+z|Learn how to solve a system with three unknowns
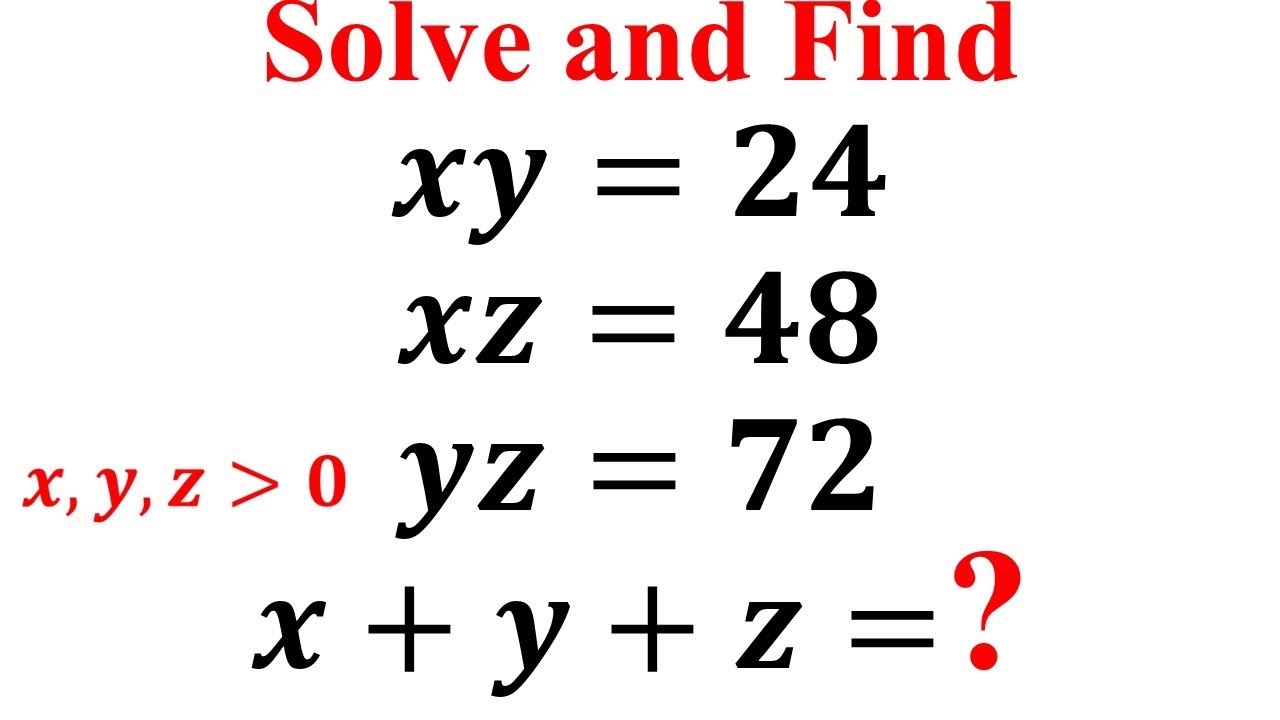
Показать описание
Finding the value of x+y+z|Learn how to solve a system with three unknowns
FInding the value of x+y+z|Learn to solve exponential equation
Nice Mathematics problem | Learn how to find value of xyz | Math Olympiad training
Solving an equation for y and x
Find the value of x+y+z (x, y, z are positive integers) || Algebra || Brainstorming Problem Series
American Mathematics Olympiad: can you find the value of xyz?
Finding Missing Angles Vertical and Supplementary Angles
Algebra Olympiad challenge--Find the value of x,y,z #olympiad#olympiadproblems
Calculus - Fundamental Theorem Of Line Integrals
Learning to Find the Value of X and Y from Congruent Triangles
How to find the value of x,y, and z using matrices..
find value of x, y, z
Nice Exponent Math Simplification | Find the Value of X,Y,Z
Mathematical Olympiad | Learn how to find the value of 123xyz/(xy+yz+zx) | Math Olympiad Training
Nice Exponent Math Simplification |Find the Value of X,Y,Z
How to find value of x y z & a in Matrix simple example
If xy = 35 , yz = 56 , zx = 40 then find the value of x , y , z | VIJAY Maths
Find the values of x, y and z from the following equations:(ii)
| Find the Value of x, y, z and u with help of given algebraic expressions |
If xy+xz+yz = 0, then what is the value of (x+y)/z + (x+z)/y + (y+z)/x ? | Algebra Challenge
Find the value of x, y & z from equation given in matrix form
IF XY = 2, XZ = 8 & YZ = 5, Then Find The Value of XYZ = ?
5 simple unsolvable equations
Part 2, Solving Using Matrices and Cramer's Rule, 3 Variables with 3 Equations
Комментарии
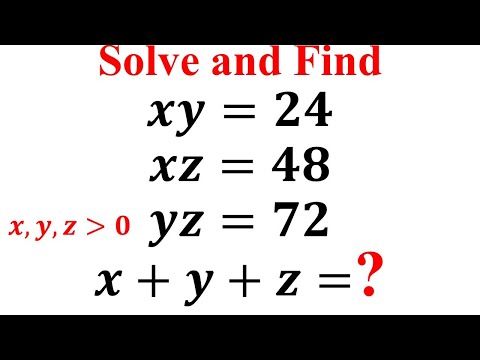 0:05:57
0:05:57
 0:06:40
0:06:40
 0:03:04
0:03:04
 0:03:47
0:03:47
 0:03:57
0:03:57
 0:06:48
0:06:48
 0:05:25
0:05:25
 0:10:31
0:10:31
 1:08:23
1:08:23
 0:02:36
0:02:36
 0:01:36
0:01:36
 0:01:56
0:01:56
 0:08:54
0:08:54
 0:08:19
0:08:19
 0:09:53
0:09:53
 0:04:45
0:04:45
 0:08:53
0:08:53
 0:04:17
0:04:17
 0:06:20
0:06:20
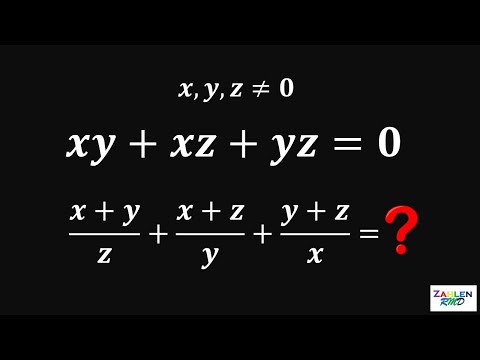 0:04:45
0:04:45
 0:05:06
0:05:06
 0:02:09
0:02:09
 0:00:50
0:00:50
 0:08:51
0:08:51