filmov
tv
Solving an Equation on Factorials of Digits | Moscow Mathematical Olympiad 1940

Показать описание
Solve Equation with Factorials
Solve Equation with Factorials
Factorials Explained!
Can You Solve this Factorial Equation? | Fast & Easy Tutorial
Factor and Solve Equation with Factorials
Equation with Factorials
how to solve a factorial equation?
equation solving☝🏻😅 #maths #factorials
FACTORIAL 1: Meaning and How to Solve Questions on Factorial. #excellenceacademy #jonahemmanuel
Solving Factorial Expressions in One Minute (2024) | Solve factorial equation
How to Solve an Equation Involving Factorials
Factorials equation #maths #matematica #algebra #equations #equazioni#factorials
a rational equation with factorials #maths #equation #solving
Solving A Cool Factorial Equation: Math behind Solution
Solving A Nice Factorial Equation
A nice factorial equation: The math behind solving equations.
Factorial Equation
A Nice Equation With Factorials @mathsmood
Solving Factorial Equation | Math Olympiad Problem
Solving an Equation on Factorials of Digits | Moscow Mathematical Olympiad 1940
Factorial Algebra Solve Equation Combinatorics
A Nice Factorial Equation
Will You Dare To Solve This Equation with Factorials ? Easy Step By Step Explanation @mathsmood
5 simple unsolvable equations
Комментарии
 0:03:25
0:03:25
 0:02:55
0:02:55
 0:11:17
0:11:17
 0:04:45
0:04:45
 0:03:41
0:03:41
 0:04:29
0:04:29
 0:02:22
0:02:22
 0:00:29
0:00:29
 0:05:06
0:05:06
 0:01:46
0:01:46
 0:05:38
0:05:38
 0:00:21
0:00:21
 0:00:32
0:00:32
 0:10:52
0:10:52
 0:03:19
0:03:19
 0:10:54
0:10:54
 0:00:49
0:00:49
 0:03:23
0:03:23
 0:05:31
0:05:31
 0:09:57
0:09:57
 0:04:26
0:04:26
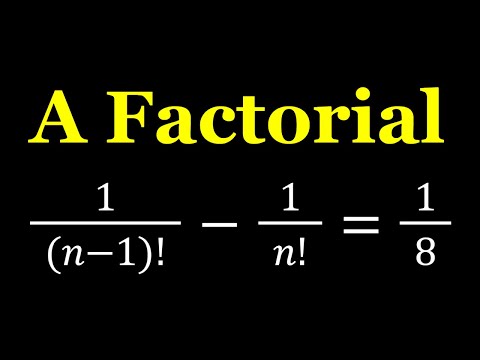 0:08:38
0:08:38
 0:04:17
0:04:17
 0:00:50
0:00:50