filmov
tv
Math Olympiad Problem | 95% Failed to solve | You should know this Trick !
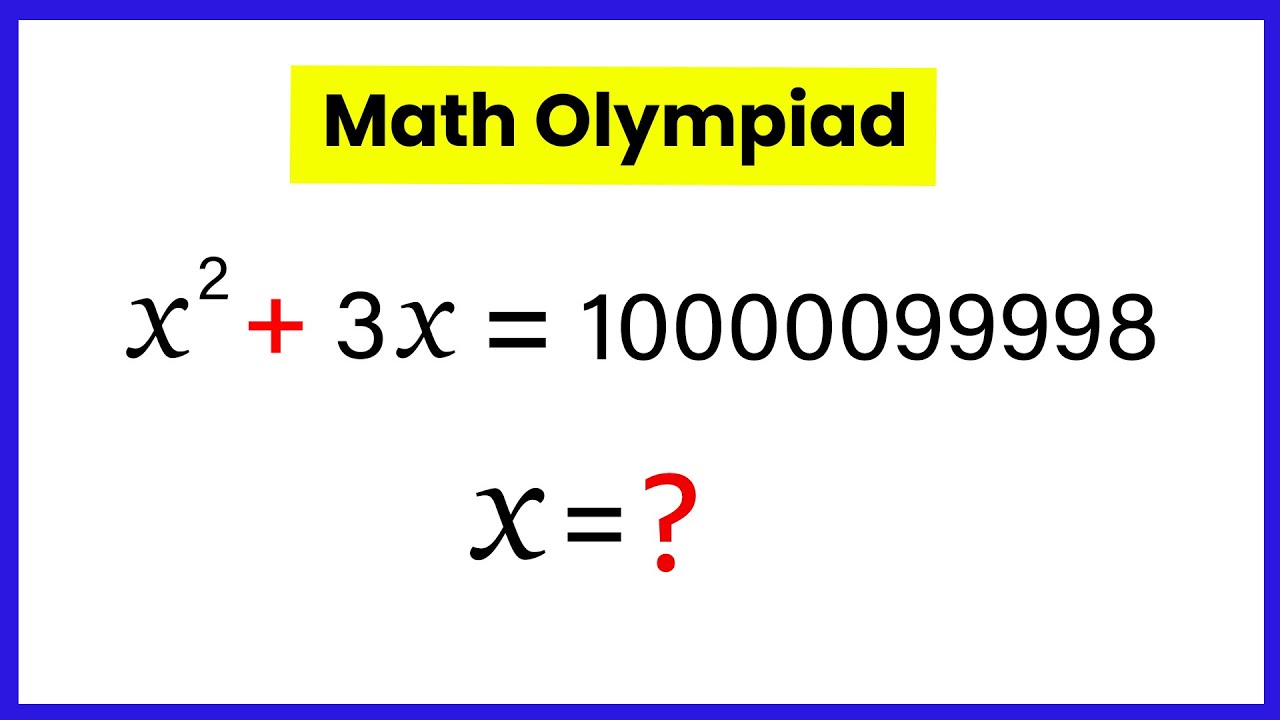
Показать описание
Also Watch our Most Viral Interesting Math Olympiad Problem:
Subscribe to our channel and press the bell icon 🔔 for daily Brainstorming Math videos →
*****************************************************************************
#exponentialproblems #matholympiad #maths
Subscribe to our channel and press the bell icon 🔔 for daily Brainstorming Math videos →
*****************************************************************************
#exponentialproblems #matholympiad #maths
1995 British Mathematics Olympiad problem
Olympiad Mathematics | 95% of the students don't know this trick
Math Olympiad Problem | Find X | x+y=95 |challenging Algebra Problem | Olympiad Mathematics
International Mathematical Olympiad (IMO) 1995 - solutions
Math Olympiad l A Nice Algebra Problem l 95% Failed to solve!
Math Olympiad Question💦95
95% couldn’t solve this math olympiad Question which was super easy😅
Math Olympiad | A Beautiful Exponential Problem | 95% aren't able to solve
Olympiad Math: Find the Number of Ordered Pairs of Integers (x, y). AIME 2000
Math Olympiad Problem | 95% Failed to solve | You should know this Trick !
Math Olympiad | A Nice Exponential Problem | 95% Failed to solve!
Germany| A very Nice Math Olympiad Problem| 95% will fail to solve this!
Math Olympiad | A Nice Exponential Problem | 95% Failed to solve!
95% Students Failed to Beat This Tricky Algebra Problem! Can You?
95% cannot solve this shape!! Lol 😝 What is the length of AB? Tricky Math Olympiad Question
Math Olympiad | A Nice Rational Equation | 95% Failed to solve!
Viral Mathematics Olympiad | 95% Can't Solve This
95% of Math Olympiad Student Failed This Geometry Question || mathstrick
Math Olympiad | A Nice Cubic Equation | 95% Failed to solve!
95% of Maths Olympiad Students Failed This Geometry Question || #mathstrick
Math Olympiad | A Nice Rational Equation | 95% Failed to solve !!
95% couldn’t solve this Math Olympiad Question
Math Olympiad | Nice Rational Equation | 95% Failed to solve!
Russian|A Very Nice Math Olympiad Problems| 95% will fail to solve this
Комментарии
 0:20:59
0:20:59
 0:10:23
0:10:23
 0:05:24
0:05:24
 0:40:44
0:40:44
 0:22:40
0:22:40
 0:10:42
0:10:42
 0:03:19
0:03:19
 0:23:41
0:23:41
 0:11:56
0:11:56
 0:14:24
0:14:24
 0:14:50
0:14:50
 0:06:12
0:06:12
 0:14:25
0:14:25
 0:12:18
0:12:18
 0:00:46
0:00:46
 0:15:43
0:15:43
 0:08:14
0:08:14
 0:00:06
0:00:06
 0:16:28
0:16:28
 0:00:06
0:00:06
 0:24:57
0:24:57
 0:05:37
0:05:37
 0:11:23
0:11:23
 0:02:53
0:02:53