filmov
tv
Math Olympiad | A Nice Exponential Problem | 95% Failed to solve!
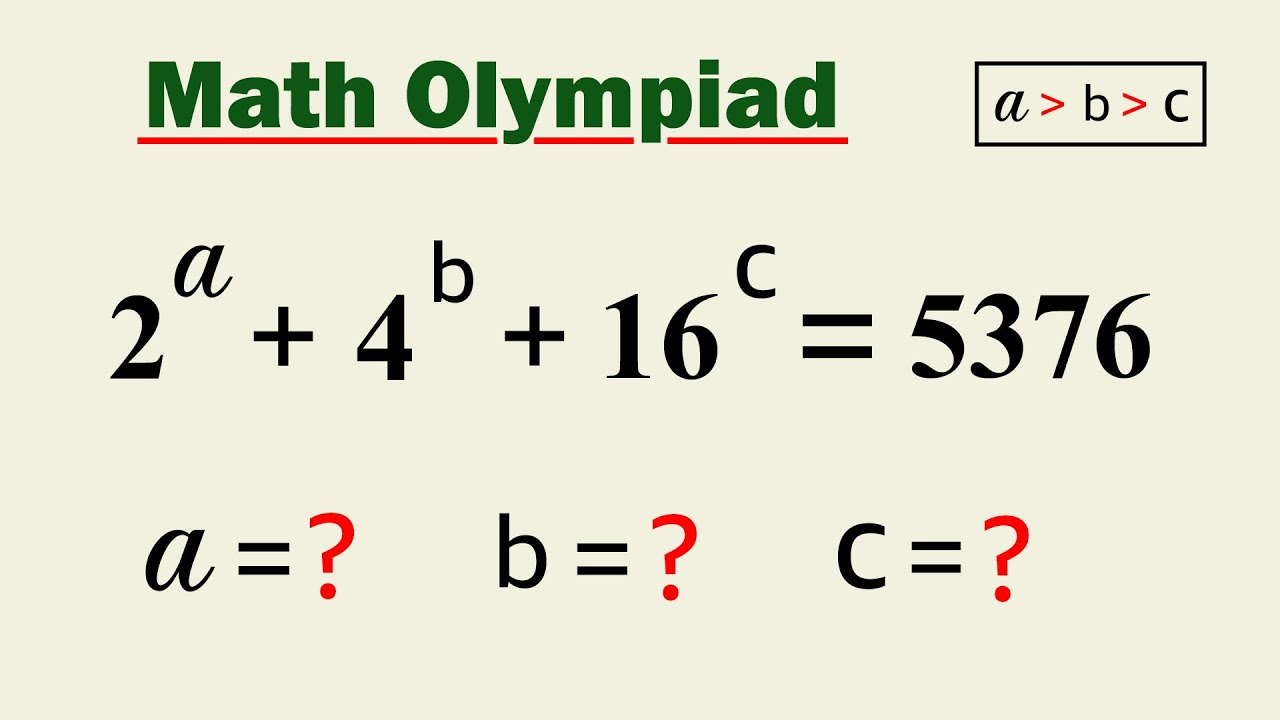
Показать описание
Also Watch our Most Viral Interesting Math Olympiad Problem:
Subscribe to our channel and press the bell icon 🔔 for daily Brainstorming Math videos →
*****************************************************************************
#exponentialproblems #matholympiad #maths
,#exponentialproblemsolving,#exponentialproblemsandsolutions,#exponentialproblemsexamples,#exponentialproblemsolvingquestions,#learnhowtosolveexponentialproblem,#aniceolympiadexponentialproblem,#exponentialfunctionproblemsolving,#exponentialgrowthanddecaywordproblems,#exponentialproblemexample,#problemsolvinginvolvingexponentialfunctions,#exponentialfunctionproblemsolvingexamples,#solvingexponentialfunctionwordproblem,#exponentialequationproblemsolving,#exponentialdecayproblemsolving,#exponentialgrowthproblem,#exponentialapplicationproblems,#exponentialdistributionproblemsandsolutions,#problemsolvingexponentialgrowthanddecay,#7.3exponentialandlogarithmicproblemsolving,#exponentialwordproblemscompoundinterest,#exponentialdecayproblem,#exponentialdecaywordproblem,#exponentialequationproblems,#exponential growth problem examples,#exponential growth example problem,#example of exponential function word problem,#word problem exponential function,#real life problem involving exponential function,#word problem involving exponential function with solution,#word problem involving exponential function,#solving real life problem involving exponential function,#exponential growth problems with solutions,#exponential growth algebra 2,#exponential word problems growth and decay,#exponential growth word problem,#howtosolveexponentialproblem,#how to solve exponential function word problem,#exponentialfunctioninproblemsolving,#problem involving exponential function,#an exponential equation,#howtosolveanexponentialfunction,#mathexponentialequation,#whatisexponentialequation,#exponentialequations # olympiad problems,#example of exponential function problem solving,#exponential means,#exponents problem solving,#exponential function word problem solving,#value of exponential e,#exponential word problem,#find x exponential equation,e exponent,#zero as an exponent,#exponential.u,#exponential times,#exponential solution,#write an exponential function,#exponential equation with e,#exponential derivatives,#exponential equalities,#exponential equation and inequality,#exponential powers,#exponents solve for x#exponentialproblems #matholympiad #maths
,#exponentialproblemsolving,#exponentialproblemsandsolutions,#exponentialproblemsexamples,#exponentialproblemsolvingquestions,#learnhowtosolveexponentialproblem,#aniceolympiadexponentialproblem,#exponentialfunctionproblemsolving,#exponentialgrowthanddecaywordproblems,#exponentialproblemexample,#problemsolvinginvolvingexponentialfunctions,#exponentialfunctionproblemsolvingexamples,#solvingexponentialfunctionwordproblem,#exponentialequationproblemsolving,#exponentialdecayproblemsolving,#exponentialgrowthproblem,#exponentialapplicationproblems,#exponentialdistributionproblemsandsolutions,#problemsolvingexponentialgrowthanddecay,#7.3exponentialandlogarithmicproblemsolving,#exponentialwordproblemscompoundinterest,#exponentialdecayproblem,#exponentialdecaywordproblem,#exponentialequationproblems,#exponential growth problem examples,#exponential growth example problem,#example of exponential function word problem,#word problem exponential function,#real life problem involving exponential function,#word problem involving exponential function with solution,#word problem involving exponential function,#solving real life problem involving exponential function,#exponential growth problems with solutions,#exponential growth algebra 2,#exponential word problems growth and decay,#exponential growth word problem,#howtosolveexponentialproblem,#how to solve exponential function word problem,#exponentialfunctioninproblemsolving,#problem involving exponential function,#an exponential equation,#howtosolveanexponentialfunction,#mathexponentialequation,#whatisexponentialequation,#exponentialequations # olympiad problems,#example of exponential function problem solving,#exponential means,#exponents problem solving,#exponential function word problem solving,#value of exponential e,#exponential word problem,#find x exponential equation,e exponent,#zero as an exponent,#exponential.u,#exponential times,#exponential solution,#write an exponential function,#exponential equation with e,#exponential derivatives,#exponential equalities,#exponential equation and inequality,#exponential powers,#exponents solve for x
Subscribe to our channel and press the bell icon 🔔 for daily Brainstorming Math videos →
*****************************************************************************
#exponentialproblems #matholympiad #maths
,#exponentialproblemsolving,#exponentialproblemsandsolutions,#exponentialproblemsexamples,#exponentialproblemsolvingquestions,#learnhowtosolveexponentialproblem,#aniceolympiadexponentialproblem,#exponentialfunctionproblemsolving,#exponentialgrowthanddecaywordproblems,#exponentialproblemexample,#problemsolvinginvolvingexponentialfunctions,#exponentialfunctionproblemsolvingexamples,#solvingexponentialfunctionwordproblem,#exponentialequationproblemsolving,#exponentialdecayproblemsolving,#exponentialgrowthproblem,#exponentialapplicationproblems,#exponentialdistributionproblemsandsolutions,#problemsolvingexponentialgrowthanddecay,#7.3exponentialandlogarithmicproblemsolving,#exponentialwordproblemscompoundinterest,#exponentialdecayproblem,#exponentialdecaywordproblem,#exponentialequationproblems,#exponential growth problem examples,#exponential growth example problem,#example of exponential function word problem,#word problem exponential function,#real life problem involving exponential function,#word problem involving exponential function with solution,#word problem involving exponential function,#solving real life problem involving exponential function,#exponential growth problems with solutions,#exponential growth algebra 2,#exponential word problems growth and decay,#exponential growth word problem,#howtosolveexponentialproblem,#how to solve exponential function word problem,#exponentialfunctioninproblemsolving,#problem involving exponential function,#an exponential equation,#howtosolveanexponentialfunction,#mathexponentialequation,#whatisexponentialequation,#exponentialequations # olympiad problems,#example of exponential function problem solving,#exponential means,#exponents problem solving,#exponential function word problem solving,#value of exponential e,#exponential word problem,#find x exponential equation,e exponent,#zero as an exponent,#exponential.u,#exponential times,#exponential solution,#write an exponential function,#exponential equation with e,#exponential derivatives,#exponential equalities,#exponential equation and inequality,#exponential powers,#exponents solve for x#exponentialproblems #matholympiad #maths
,#exponentialproblemsolving,#exponentialproblemsandsolutions,#exponentialproblemsexamples,#exponentialproblemsolvingquestions,#learnhowtosolveexponentialproblem,#aniceolympiadexponentialproblem,#exponentialfunctionproblemsolving,#exponentialgrowthanddecaywordproblems,#exponentialproblemexample,#problemsolvinginvolvingexponentialfunctions,#exponentialfunctionproblemsolvingexamples,#solvingexponentialfunctionwordproblem,#exponentialequationproblemsolving,#exponentialdecayproblemsolving,#exponentialgrowthproblem,#exponentialapplicationproblems,#exponentialdistributionproblemsandsolutions,#problemsolvingexponentialgrowthanddecay,#7.3exponentialandlogarithmicproblemsolving,#exponentialwordproblemscompoundinterest,#exponentialdecayproblem,#exponentialdecaywordproblem,#exponentialequationproblems,#exponential growth problem examples,#exponential growth example problem,#example of exponential function word problem,#word problem exponential function,#real life problem involving exponential function,#word problem involving exponential function with solution,#word problem involving exponential function,#solving real life problem involving exponential function,#exponential growth problems with solutions,#exponential growth algebra 2,#exponential word problems growth and decay,#exponential growth word problem,#howtosolveexponentialproblem,#how to solve exponential function word problem,#exponentialfunctioninproblemsolving,#problem involving exponential function,#an exponential equation,#howtosolveanexponentialfunction,#mathexponentialequation,#whatisexponentialequation,#exponentialequations # olympiad problems,#example of exponential function problem solving,#exponential means,#exponents problem solving,#exponential function word problem solving,#value of exponential e,#exponential word problem,#find x exponential equation,e exponent,#zero as an exponent,#exponential.u,#exponential times,#exponential solution,#write an exponential function,#exponential equation with e,#exponential derivatives,#exponential equalities,#exponential equation and inequality,#exponential powers,#exponents solve for x
Комментарии
 0:10:09
0:10:09
 0:00:52
0:00:52
 0:09:23
0:09:23
 0:02:34
0:02:34
 0:09:23
0:09:23
 0:13:13
0:13:13
 0:01:00
0:01:00
 0:11:51
0:11:51
 0:07:04
0:07:04
 0:10:37
0:10:37
 0:00:51
0:00:51
 0:11:45
0:11:45
 0:15:00
0:15:00
 0:00:33
0:00:33
 0:00:10
0:00:10
 0:12:03
0:12:03
 0:01:26
0:01:26
 0:08:36
0:08:36
 0:02:51
0:02:51
 0:12:39
0:12:39
 0:10:07
0:10:07
 0:07:53
0:07:53
 0:06:59
0:06:59
 0:15:05
0:15:05