filmov
tv
Introduction to the Weierstrass Substitution

Показать описание
In this video, we look at the Weierstrass substitution, a very useful type of substitution discovered by mathematician Karl Weierstrass, which is also known as the tangent half-angle substitution. We take a substitution which will simplify integrals of rational expressions of trigonometric functions, which is some variable t = tan(x/2), hence the name half-angle substitution.
We then solve for dx and the necessary trigonometric functions in terms of t, which all work out to make the integral easier as they all have the same denominator, which can reduce a lot of integrals in this form to just algebraic manipulation or a simple partial fraction decomposition in terms of t. We then close by looking at a practice integral question in which we can utilize the Weierstrass substitution to show the power of the method. Try the integral before you watch the solution as well:
∫1/(2+cos(x)) dx
If this was the integral of 1/(1+cos(x)) that would be quite simple as you can multiply by the conjugate and get a very simple integral, however, where the Weierstrass displays its capability, is when you have a constant other than 1 in this form.
Thanks for watching
We then solve for dx and the necessary trigonometric functions in terms of t, which all work out to make the integral easier as they all have the same denominator, which can reduce a lot of integrals in this form to just algebraic manipulation or a simple partial fraction decomposition in terms of t. We then close by looking at a practice integral question in which we can utilize the Weierstrass substitution to show the power of the method. Try the integral before you watch the solution as well:
∫1/(2+cos(x)) dx
If this was the integral of 1/(1+cos(x)) that would be quite simple as you can multiply by the conjugate and get a very simple integral, however, where the Weierstrass displays its capability, is when you have a constant other than 1 in this form.
Thanks for watching
 0:07:17
0:07:17
 0:10:24
0:10:24
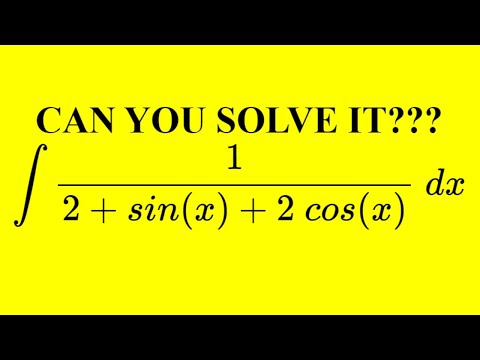 0:07:12
0:07:12
 0:16:22
0:16:22
 0:10:21
0:10:21
 0:13:13
0:13:13
 0:04:46
0:04:46
 0:08:32
0:08:32
 0:05:06
0:05:06
 0:04:55
0:04:55
 0:13:45
0:13:45
 0:13:36
0:13:36
 0:01:36
0:01:36
 0:35:43
0:35:43
 0:09:43
0:09:43
 0:23:41
0:23:41
 0:08:11
0:08:11
 0:06:08
0:06:08
 0:19:11
0:19:11
 0:27:37
0:27:37
 0:06:01
0:06:01
 0:06:00
0:06:00
 0:10:05
0:10:05
 0:10:04
0:10:04