filmov
tv
Limits are unique

Показать описание
Limits are unique
In this video, I show that limits are unique. In other words, a convergent sequence must converge to exactly one number, it cannot have two different limits. And of course, what makes this so elegant is the proof, this is analysis at its finest, enjoy! :)
Other examples of limits can be seen in the playlist below.
In this video, I show that limits are unique. In other words, a convergent sequence must converge to exactly one number, it cannot have two different limits. And of course, what makes this so elegant is the proof, this is analysis at its finest, enjoy! :)
Other examples of limits can be seen in the playlist below.
Proof: Limit of a Function is Unique | Real Analysis
Proof: The Limit of a Sequence is Unique | Real Analysis
Limits are unique
The Limit of a Sequence is Unique Proof
Real Analysis Course #18 - Sequence Limits are Unique Proof
Limits Are Unique
When a limit exists, It is Unique - Proof
Limits & Continuity Explained in 10 Minutes Through Song!
ANIMATION VIDEO(ANIMATION)
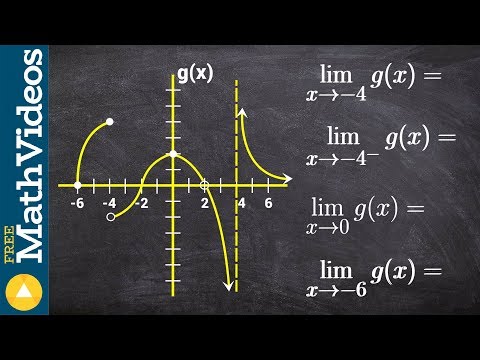
How To Evaluate Limits From a Graph
Real Analysis, Lecture 5 (Convergence and limits of sequences)
Lecture 3.5 - Uniqueness of Limits
Sequence Limits Are Like Snowflakes - They're Unique
Sequence Limits Are Like Snowflakes - They're Unique
Limits of Multivariable Functions - Calculus 3
Infinite Limits With Equal Exponents (Calculus)
Lecture 15: Limits of Functions
Evaluate all the limits from a given graph
Lisa Bevere: This Limits YOUR Unique Calling | Women of Faith on TBN
7.4 Uniqueness of limits
12 Unique Smartphone Features & Designs That Flopped
Limits of Sequences
Uniqueness of limits of sequences in Hausdorff space
Limits in a metric space are unique or sequence in a metric space converges to only one point Hindi
Комментарии
 0:06:25
0:06:25
 0:13:22
0:13:22
 0:07:42
0:07:42
 0:05:14
0:05:14
 0:05:35
0:05:35
 0:07:48
0:07:48
 0:09:56
0:09:56
 0:10:37
0:10:37
 0:00:27
0:00:27
 0:11:32
0:11:32
 0:47:34
0:47:34
 0:18:24
0:18:24
 0:15:29
0:15:29
 0:22:35
0:22:35
 0:19:04
0:19:04
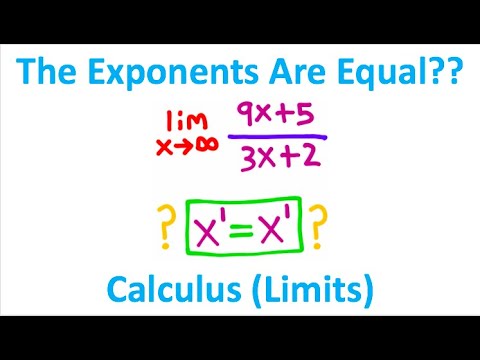 0:00:49
0:00:49
 0:43:13
0:43:13
 0:05:34
0:05:34
 0:11:56
0:11:56
 0:06:24
0:06:24
 0:10:37
0:10:37
 0:54:40
0:54:40
 0:07:37
0:07:37
 0:16:14
0:16:14