filmov
tv
Understanding an elementary proof of prime number theorem in full details from scratch in six hours
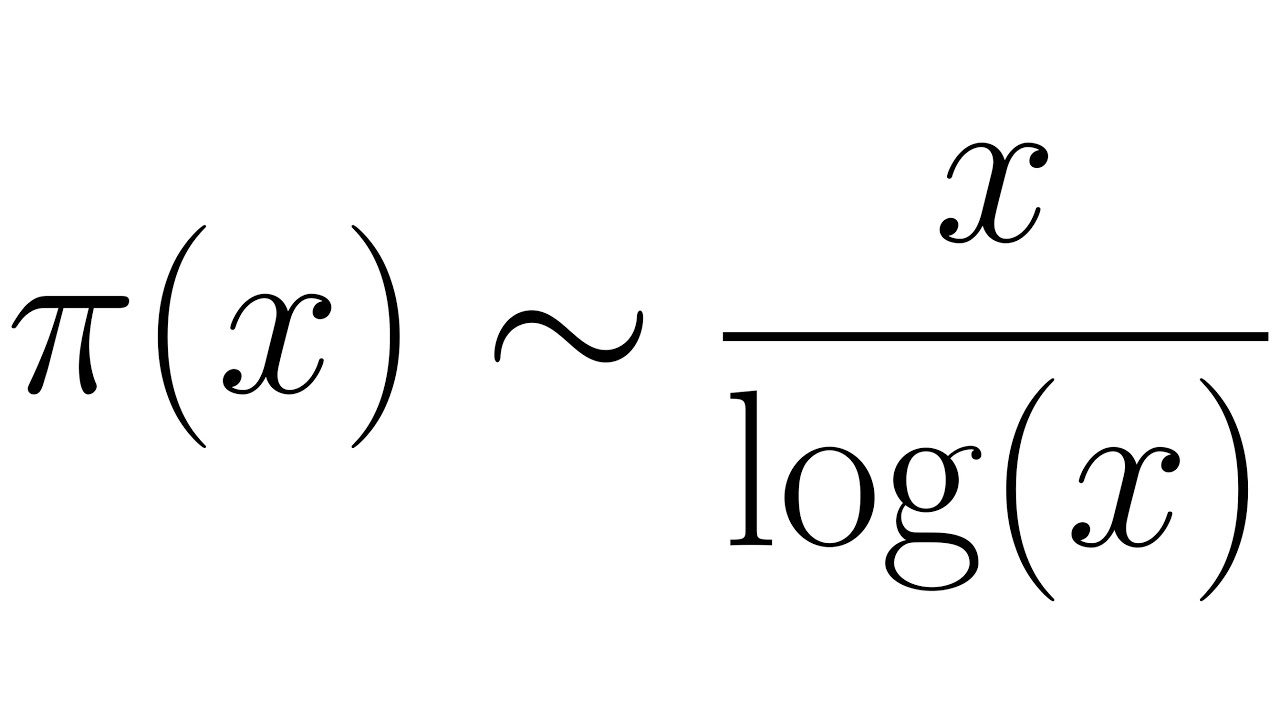
Показать описание
This video series features the elementary proof of prime number theory (PNT) following Hardy's book "An Introduction to the Theory of Numbers" (in the spirit of Erdos and Selberg), targeting ambitious high school students, undergraduate students as well as graduate students who need to watch something to help them fall asleep faster at night. The audience are only assumed to know calculus, basic combinatorics (binomial theorem) and basic elementary number theory (prime numbers and prime decomposition). No prior knowledge of complex analysis (we won't need it) or arithmetic functions (will be introduced from scratch) is required. "Six hours" might be exaggerating to smart people since I believe you could play at 1.25x speed or even 1.5x speed. If you prefer to watch this piece by piece, a playlist of 20 short video sections can be found here:
Understanding an elementary proof of prime number theorem in full details from scratch in six hours
Josef Teichmann: An elementary proof of the reconstruction theorem
iNT 04 05 An Elementary Proof of Fermat's Little Theorem
Elementary proof
How many ways are there to prove the Pythagorean theorem? - Betty Fei
Differential equations, a tourist's guide | DE1
Dividing by Zero in Five Levels -- Elementary to Math Major
iNT 04 09 An Elementary Proof of Wilson's Theorem
Group Theory Lecture 1.3 Elementary Properties of Groups
elementary proof of polignac's conjecture
Claims, Evidence, and Reasoning.
Gauss' Multiplication Formula - An Elementary Proof without Stirling!
Proof by Contradiction | Method & First Example
An elementary proof of Conway's theorem on Rational Tangles (Part 1)
Understanding Elementary Calculus: Principles, Problems, and Solutions
What does a ≡ b (mod n) mean? Basic Modular Arithmetic, Congruence
Negative × Negative = Positive in 5 Levels -- Elementary to Math Major
Elementary Algebra
Elementary Proof of Euclid's Theorem
Makes me feel old #fyp #reading #elementary #school #hamilton #funny
DIRECT PROOFS - DISCRETE MATHEMATICS
Elementary proof of prime number theorem 20 the end
sin(n) does not converge - an elementary proof
Fact vs. Theory vs. Hypothesis vs. Law… EXPLAINED!
Комментарии
 5:49:24
5:49:24
 0:46:46
0:46:46
 0:12:43
0:12:43
 0:03:44
0:03:44
 0:05:17
0:05:17
 0:27:16
0:27:16
 0:06:49
0:06:49
 0:10:15
0:10:15
 0:54:35
0:54:35
 0:00:16
0:00:16
 0:02:06
0:02:06
 0:29:19
0:29:19
 0:09:00
0:09:00
 0:50:54
0:50:54
 0:03:25
0:03:25
 0:05:45
0:05:45
 0:08:02
0:08:02
 0:05:35
0:05:35
 0:07:06
0:07:06
 0:00:18
0:00:18
 0:07:24
0:07:24
 0:35:44
0:35:44
 0:13:39
0:13:39
 0:07:00
0:07:00